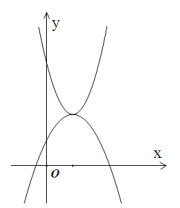①bc>0;②2a+b>0;③a+b+c>0;④方程ax2+ bx+c=0有一个正根和一个负根;⑤当x >1时,y随x的增大而减小。

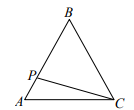
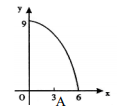 B .
B . 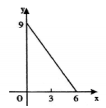 C .
C . 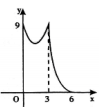 D .
D . 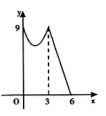

甲:对称轴为直线x=2;
乙:与x轴两个交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.
请你写出满足上述全部特点的一个二次函数解析式
|
抽取球数 |
50 |
100 |
500 |
1000 |
5000 |
|
优等品数 |
45 |
92 |
455 |
890 |
4500 |
|
优等品频率 |
|
|
|
|
|