浙江省湖州市吴兴区2020年数学中考一模试卷

更新时间：2021-02-22 浏览次数：532 类型：中考模拟

一、选择题（本题有10小题，每小题3分，共30分）

1. (2020·吴兴模拟) 在 $\text{[math]}$ 这四个数中，最小的数是（）

A . $\text{[math]}$ B . 0 C . -3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·吴兴模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·玉山期末) 小刚和小亮分别统计了自己最近50次跳绳成绩，下列统计量中能用来比较两人成绩稳定程度的是（）

A . 方差 B . 中位数 C . 平均数 D . 众数

答案解析收藏纠错 + 选题
4. (2022九上·邯山期末) 一个布袋里装有2个白球和3个黑球，它们除颜色外其余都相同，从袋子里任意摸出1个球，摸到黑球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
5. (2023·金山模拟) 在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，tanB＝（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·吴兴模拟) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2020·吴兴模拟) 如图，在平面直角坐标系中，正方形 ABCO 的顶点 A，C 分别在 y 轴、x 轴上，以 AB 为弦的⊙M 与 x 轴相切，若点 A 的坐标（0，8），则圆心M 的坐标为（）

A . （－4，3） B . （－3，4） C . （－5，5） D . （－4，5）

答案解析收藏纠错 + 选题
8. (2024九上·泸县模拟) 抛物线经过点A(2,0),B(−1,0),且与y轴交于点C,若OC=2.则该抛物线解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·吴兴模拟) 如图，以矩形OABC的两边OA和OC所在直线为x轴、y轴建立平面直角坐标系。将矩形OABC绕点O逆时针旋转30°，得到矩形ODEF，若当点A的坐标为（- $\text{[math]}$ ， 0）时，反比例函数 $\text{[math]}$ 的图象恰好经过B、F两点，则此时k的值为（）.

A . $\text{[math]}$ B . -6 C . $\text{[math]}$ D . -3

答案解析收藏纠错 + 选题
10. (2020·吴兴模拟) 如图，在矩形ABCD中，点E，F将对角线AC三等分，已知 AB＝9，BC＝12，点P在矩形ABCD的边上，则满足PE+PF＝12的点P的个数是（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2024七上·江南期中) 8的立方根为.

答案解析收藏纠错 + 选题
12. (2024九上·良庆开学考) 因式分解： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
13. (2020·吴兴模拟) 一个扇形的半径是12cm，面积是 $\text{[math]}$ ，则此扇形的圆心角的度数是．

答案解析收藏纠错 + 选题
14. (2020·吴兴模拟) 如图所示，把菱形ABCD沿折痕AH翻折，使B点落在BC延长线上的点E处，连结DE．若∠B＝30°，则∠ADE＝．

答案解析收藏纠错 + 选题
15. (2020·吴兴模拟) 正方形ABCD，点E在BC上，点F在CD上，且BE=CF.连结AE，BF，两线相交于点G，已知正方形边长为 $\text{[math]}$ ，△ABG的周长为 $\text{[math]}$ ，则图中阴影部分与空白部分的面积比为.

答案解析收藏纠错 + 选题
16. (2020·吴兴模拟) 在滑草过程中，小明发现滑道两边形如两条双曲线。如图，点A₁ ， A₂ ， A₃…在反比例函数 $\text{[math]}$ 的图象上，点B₁ ， B₂ ， B₃…在反比例函数 $\text{[math]}$ 的图象上， A₁B₁//A₂B₂…//y轴，已知点A₁ ， A₂…的横坐标分别为1 ， 2 …，令四边形A₁B₁B₂A₂、A₂B₂B₃A₃、 …的面积分别为S₁、S₂、…
1. （1）用含m、n的代数式表示S₁₌ ．
2. （2）若S₂₀=41，则n-m=．
答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共66分）

17. (2020·吴兴模拟) 计算：＋( ) ＋ cos30°．

答案解析收藏纠错 + 选题
18. (2020·吴兴模拟) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2020·吴兴模拟) 如图，一次函数 $\text{[math]}$ 的图象与x轴，y轴分别交于A（-12，0），B（0，6）两点。
1. （1）求一次函数的解析式；
2. （2）若C为x轴上任意一点，使得△ABC的面积为6求点C的坐标；
答案解析收藏纠错 + 选题
20. (2020·吴兴模拟) 某报社为调查湖州市民对大范围雾霾天气的成因、影响以及应对措施的了解程度，做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了不完整的三种统计图表．请结合统计图表，回答下列问题．

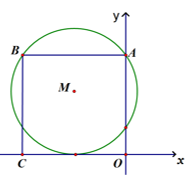
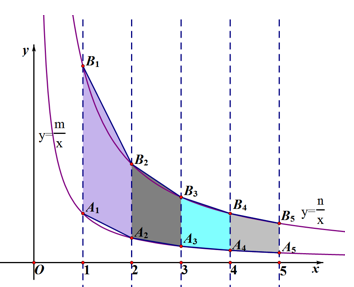
对雾霾的了解程度百分比

A 非常了解 5%

B 比较了解 m%

C 基本了解 45%

D 了解 n%
1. （1）本次参与调查的市民共有人，m=，n=；
2. （2）图 2所示的扇形统计图中 D部分扇形所对应的圆心角是度；
3. （3）根据调查结果．学校准备开展关于雾霾知识竞赛，某班要从小明和小刚中选一人参加，现设计了如下游戏来确定：在一个不透明的袋中装有 2个红球和 3个白球，它们除了颜色外都相同，小明先从袋中随机摸出一个球，小刚再从剩下的四个球中随机摸出一个球，若摸出的两个球颜色相同，则小明去；否则小刚去．现在，小明同学摸出了一个白球，则小明参加竞赛的概率为多少？
答案解析收藏纠错 + 选题
21. (2020·吴兴模拟) 如图，AB是⊙O的直径，BC⊥AB，弦AD∥OC。
1. （1）求证：DC是⊙O的切线
2. （2）已知AB=6，CB=4，求线段AD的长
答案解析收藏纠错 + 选题
22. (2020·吴兴模拟) 某工厂上班高峰期员工到达单位的累积人数y随时间x的变化情况如图所示，已知前10分钟，y可看作是x的二次函数，并在10分钟时，累计到达人数为最大值500人，10分钟之后员工全部到岗，累计人数不变。回答下列问题：
1. （1）求出0-10分钟内，y与x之间的函数解析式；
2. （2）受新型冠状病毒影响，员工在进入单位大门时都应该配合监测体温。如果员工一到达工厂大门就开始接受体温测量，工厂大门口有体温检测岗位2个，每个岗位的工作人员每分钟检测10人，问：工厂门口等待接受体温测量的队伍最多时有多少人；
3. （3）在（1）（2）的前提下，员工检测体温到第5分钟时，为提高通过效率，减缓拥堵情况，如果要在接下来的10分钟内让全部到达等待的员工都能完成体温检测，问：此时需至少增设几个体温检测岗位？
答案解析收藏纠错 + 选题
23. (2020·吴兴模拟) 如图
1. （1）【问题探究】
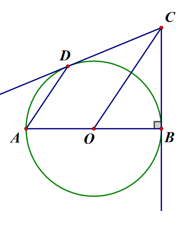
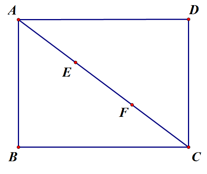
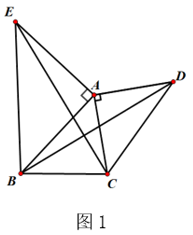
  如图1，锐角△ABC中，分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD＝90°，连接BD，CE，试猜想BD与CE的大小关系，不需要证明．
2. （2）【深入探究】
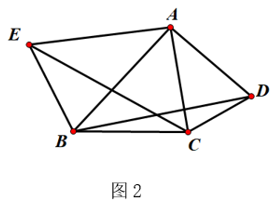
  如图2，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD，连接BD、CE，试猜想BD与CE的大小关系，并说明理由．
3. （3）【拓展应用】
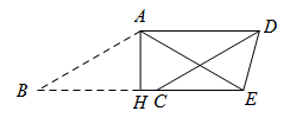
  如图3，在△ABC中，∠ACB=45°，以AB为直角边，A为直角顶点向外作等腰直角△ABD，连接CD，若AC= $\text{[math]}$ ，BC=3，则CD长为.
4. （4）如图4，已知在平面直角坐标系xOy中，O为坐标原点，A（0， $\text{[math]}$ ）、P（3，0），过点P作直线l⊥x轴，点B是直线l上的一个动点，线段AB绕点A按逆时针方向旋转30°得到线段AC．则AC+PC的最小值为．
答案解析收藏纠错 + 选题
24. (2020·吴兴模拟) 在平面直角坐标系中，抛物线C_外： $\text{[math]}$ ，抛物线C_内： $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，且C_内的图象经过点A（- 3，- 2），动直线 $\text{[math]}$ 与抛物线C_内交于点M，与抛物线C_外交于点N。
1. （1）求抛物线C_内的表达式；
2. （2）当△AMN是以MN为直角边的等腰直角三角形时，求 $\text{[math]}$ 的值；
3. （3）在（2）的条件下，设抛物线C_外与y轴交于点B，连结AM交y轴于点P，连结PN。
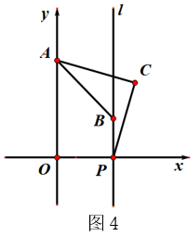
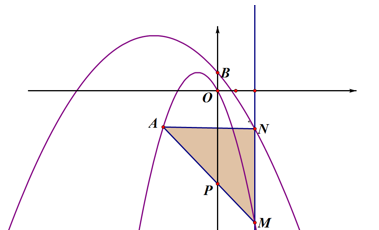
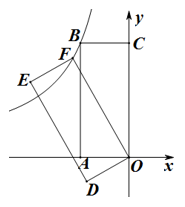
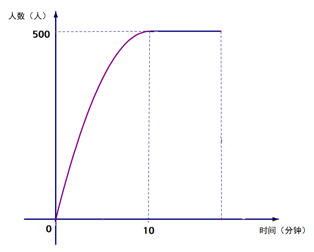
  ①在P点上方的y轴上是否存在点K，使得∠KNP=∠ONB？若存在，求出点K的坐标，若不存在，说明理由。
  
  ②若平面内有一点G，且PG=1，是否存在这样的点G，使得∠GNP=∠ONB？若存在，直接写出点G的坐标，若不存在，说明理由。
答案解析收藏纠错 + 选题