浙江省宁波市镇海区2020-2021学年八年级上学期数学期中...

更新时间：2021-05-20 浏览次数：303 类型：期中考试

一、选择题（每小题3分，共36分）

1. (2020八上·镇海期中) 下列防疫图标中的图形是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020八上·镇海期中) 三角形的两边长分别是5和7，则第三边长不可能是（）

A . 6 B . 8 C . 9 D . 12

答案解析收藏纠错 + 选题
3. (2020八上·镇海期中) 若 $\text{[math]}$ ，运用不等式的性质，下列各式中变形一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020八上·镇海期中) 直角三角形两条直角边长分别是5和12，则第三边上的中线长为（）

A . 6 B . 6.5 C . 8 D . 10

答案解析收藏纠错 + 选题
5. (2022八上·柳城期中) 已知等腰三角形的一个角是100°，则它的底角是（）

A . 40° B . 60° C . 80° D . 40°或100°

答案解析收藏纠错 + 选题
6. (2020八上·镇海期中) 下列问题的解答正确的是（）

A . m的3倍不大于n的 $\text{[math]}$ ，可表示为3m＜ $\text{[math]}$ B . $\text{[math]}$ $\text{[math]}$ ≥0 C . a是非负数，可表示为a＞0 D . $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020八上·夏津期中) 如图，在△ABC中，AD⊥BC ， AE平分∠BAC ，若∠BAE＝30°，∠CAD＝20°，则∠B＝（）

A . 45° B . 60° C . 50° D . 55°

答案解析收藏纠错 + 选题
8. (2020八上·镇海期中) 下列命题的逆命题是真命题的是（）

A . 对顶角相等 B . 若一个三角形的两个内角分别为30°和60°，则这个三角形是直角三角形 C . 两个全等的三角形面积相等 D . 直角三角形斜边上的中线等于斜边的一半

答案解析收藏纠错 + 选题
9. (2020八上·镇海期中) 若△ABC三边长a，b，c满足|a²-b²|+(c-a)²=0，则△ABC是（）

A . 直角三角形 B . 等边三角形 C . 等腰三角形 D . 等腰直角三角形

答案解析收藏纠错 + 选题
10. (2020八上·镇海期中) 如图，所示的正方形网格中，网格线的交点称为格点.已知A、B两点为格点，如果C也是图中的格点，则满足△ABC为等腰三角形的点C的个数为（）

A . 6个 B . 7个 C . 8个 D . 9个

答案解析收藏纠错 + 选题
11. (2023七下·宁阳期末) 如图，在已知的△ABC中，按以下步骤作图：
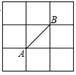
①分别以B，C为圆心，以大于 $\text{[math]}$ BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（）

A . 90° B . 95° C . 100° D . 105°

答案解析收藏纠错 + 选题
12. (2020八上·镇海期中) 如图，D，E分别是△ABC的边AB、BC上的点，AD＝2BD，BE＝CE，设△ADF的面积为S₁ ， △CEF的面积为S₂ ，若S_△ABC＝12，则S₁﹣S₂＝（）

A . 1.5 B . 2 C . 3 D . 0.5

答案解析收藏纠错 + 选题

二、填空题 (每小题3分，共18分)

13. (2020八上·镇海期中) 在△ABC中，∠C=90°，∠A:∠B=1: 2，则∠B=.

答案解析收藏纠错 + 选题
14. (2020八上·镇海期中) 把命题：“内错角相等”改写成“如果......那么......”的形式是.

答案解析收藏纠错 + 选题
15. (2020八上·镇海期中) 如图，在Rt△ABC与Rt△DCB中，已知∠A＝∠D＝90°，请你添加一个条件（不添加字母和辅助线），使Rt△ABC≌Rt△DCB，你添加的条件是（填一个即可）.

答案解析收藏纠错 + 选题
16. (2020八上·镇海期中) 若x＞y，且（m-5）x ＜（m-5）y ，则m的取值范围是.

答案解析收藏纠错 + 选题
17. (2020八上·镇海期中) 一个等腰三角形的底边长为5，一条腰上的中线把周长分成的两部分的差为2，则这个等腰三角形的腰长为.

答案解析收藏纠错 + 选题
18. (2020八上·镇海期中) 如图，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC外，若∠2＝18°，则∠1的度数为.

答案解析收藏纠错 + 选题

三、解答题（第

19. (2020八上·镇海期中) 在不同的数轴上表示下列不等式，并分别写出满足不等式的所有负整数。
1. （1） x＞ $\text{[math]}$ 2
2. （2） -2≤x＜1
答案解析收藏纠错 + 选题
20. (2020八上·镇海期中) 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形：
1. （1）在图（1）中，画一个直角三角形，使它的三边长都是有理数；
2. （2）在图（2）中，画一个等腰直角三角形，使它的三边长都是无理数；
3. （3）在图（3）中，画一个正方形，使它的面积是8.
答案解析收藏纠错 + 选题
21. (2020八上·镇海期中) 某数学兴趣小组在学习“不等式的性质”时，有两名同学的对话如下：

你认为小英和小亮的结论正确吗？如果正确，请说明理由；如果不正确，请举出一个反例。

答案解析收藏纠错 + 选题
22. (2021八上·沈阳月考) 如图，在一条东西走向河流的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H（A、H、B在同一条直线上），并新修一条路CH，测得CB＝1.5千米，CH＝1.2千米，HB＝0.9千米.
1. （1）问CH是否为从村庄C到河边的最近路？请通过计算加以说明；
2. （2）求新路CH比原路CA少多少千米？
答案解析收藏纠错 + 选题
23. (2022九下·黄石开学考) 如图，∠1=∠2，AD=AE，∠B=∠ACE，且B、C、D三点在一条直线上，
1. （1）试说明△ABD与△ACE全等的理由；
2. （2）如果∠B=60°，试说明线段AC、CE、CD之间的数量关系，并说明理由.
答案解析收藏纠错 + 选题
24. (2020八上·镇海期中) 某水果批发站购进苹果和梨共100箱，其中苹果每箱40元，梨每箱45元。
1. （1）若设苹果箱数为x箱，总费用为y元，试用x的代数式来表示总费用y.
2. （2）若购进的100箱水果中，苹果箱数不小于30箱，且不大于90箱，试求该水果批发站此次购入水果的总费用的范围.
答案解析收藏纠错 + 选题
25. (2020八上·镇海期中) 定义：线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”.试解答下列问题：
1. （1）在图1中，∠A、∠B、∠C、∠D之间的关系为.
2. （2）如图2，在（1）的结论下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于点M、N.
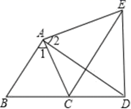
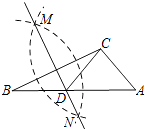
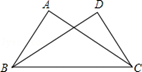
  ①仔细观察，在图2中有 ▲ 个以线段AD为边的“8字形”；
  
  ②若∠D＝40°，∠B＝36°，试求∠P的度数（请说明理由）；
  
  ③∠D和∠B为任意角时，其他条件不变，试直接写出∠P与∠D、∠B之间的数量关系，不需说明理由.
答案解析收藏纠错 + 选题
26. (2020八上·镇海期中) 阅读下列材料，解决提出的问题：

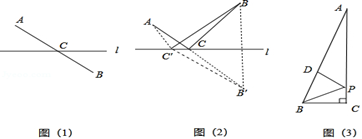
【最短路径问题】

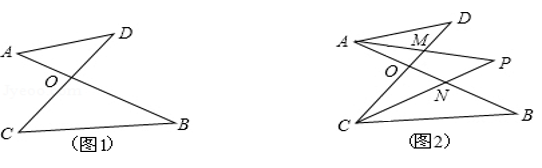
如图（1），点A，B分别是直线l异侧的两个点，如何在直线l上找到一个点C，使得点C到点A，点B的距离和最短？我们只需连接AB，与直线l相交于一点，可知这个交点即为所求.

如图（2），如果点A，B分别是直线l同侧的两个点，如何在l上找到一个点C，使得这个点到点A、点B的距离和最短？我们可以利用轴对称的性质，作出点B关于的对称点B’，这时对于直线l上的任一点C，都保持CB＝CB’，从而把问题（2）变为问题（1）.因此，线段AB’与直线l的交点C的位置即为所求.

为了说明点C的位置即为所求，我们不妨在直线上另外任取一点C’，连接AC’，BC’，B’C’.

因为AB’≤AC’+C’B’ ， ∴AC+CB≤AC’+C’B，即AC+BC最小.
1. （1）【数学思考】
  材料中划线部分的依据是.
2. （2）材料中解决图（2）所示问题体现的数学思想是 .（填字母代号即可）
  
  A . 转化思想 B . 分类讨论思想 C . 整体思想
3. （3）【迁移应用】
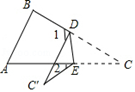
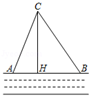
  如图3，在Rt△ABC中，∠C＝90°，∠BAC＝15°，点P为C边上的动点，点D为AB边上的动点，若AB＝6cm，求BP+DP的最小值.
答案解析收藏纠错 + 选题