


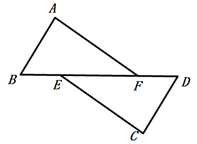
①BD=CE; ②BD⊥CE; ③∠ACE+∠DBC=45°;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )


|
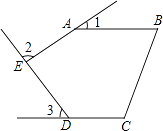
如图,在等边三角形 |
 小华与同桌小明讨论后,进行了如下解答
小华与同桌小明讨论后,进行了如下解答
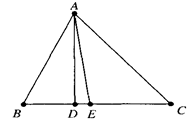
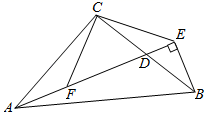
当点E为 的中点时,如图1,确定线段
与
的大小关系.请你直接写出结论:
(填“
”,“
”或“
”)
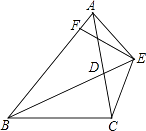
对原题中的一般情形,二人讨论后得出(1)中的结论仍然成立,并且可以通过构造一个三角形与 全等来证明.以下是他们的部分证明过程:
证明:如图2,过点E作 ,交
于点F.(请完成余下的证明过程)

在边长为 的等边三角形
中,点E在直线
上,且
,点D在直线
上,
.则
(直接写出结果)
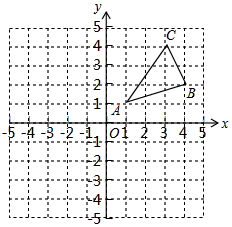
⑴画出△ABC关于y轴的对称图形△A1B1C1 , 并写出点B1的坐标;
⑵在x轴上求作一点P , 使△PAB的周长最小,并直接写出点P的坐标.
如图1, 与
均是顶角为
的等腰三角形,
,
分别是底边,求证:
;

图1
如图2, 与
均为等边三角形,点A,D,E在同一直线上,连接
填空: 的度数为,线段
与
之间的数量关系为.
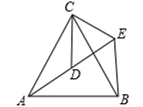
图2
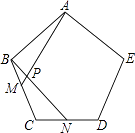
如图3, 与
均为等腰直角三角形,
,点A,D,E在同一直线上,
于点M,连接
.请求出
的度数及线段
,
,
之间的数量关系,并说明理由.

图3