


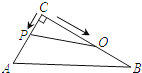
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是( )
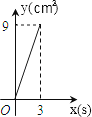 B .
B . 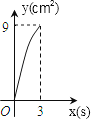 C .
C . 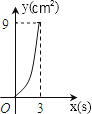 D .
D . 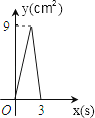
①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣ ,y1),(
,y2)是抛物线上的两点,则y1>y2 , 其中说法正确的是( )


综上所述,原方程的解是 或
.
依照上例解法,解方程 .