河南省2021届高三下学期理数高考适应性考试试卷

更新时间：2021-04-22 浏览次数：156 类型：高考模拟

一、单选题

1. (2021·河南模拟) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·河南模拟) 已知复数 $\text{[math]}$ 满足 $\text{[math]}$ （其中 $\text{[math]}$ 为虚数单位），则复数 $\text{[math]}$ 的虚部为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022高二下·安康期末) 若函数 $\text{[math]}$ 的最大值为 $\text{[math]}$ ，则常数 $\text{[math]}$ 的一个可能取值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·河南模拟) 若实数 $\text{[math]}$ 满足 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·河南模拟) 如图，圆锥的轴截面ABC为正三角形，其面积为 $\text{[math]}$ ，D为弧AB的中点，E为母线BC的中点，则异面直线 $\text{[math]}$ 所成角的余弦值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·河南模拟) 已知点 $\text{[math]}$ 为抛物线 $\text{[math]}$ 上任意一点，点 $\text{[math]}$ 是圆 $\text{[math]}$ 上任意一点，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·河南模拟) “中国剩余定理”又称“孙子定理”，讲的是关于整除的问题.现有这样一个整除问题：将1到2021这2021个正整数中能被3除余1且被5除余1的数按从小到大的顺序排成一列，构成数列 $\text{[math]}$ ，则数列 $\text{[math]}$ 各项的和为（）

A . 137835 B . 137836 C . 135809 D . 135810

答案解析收藏纠错 + 选题
8. (2021·河南模拟) 从正方体的12条棱中任选3条棱，则这3条棱两两异面的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021高一下·泾县月考) 若 $\text{[math]}$ 的外心为 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 5 B . 8 C . 10 D . 13

答案解析收藏纠错 + 选题
10. (2021·河南模拟) 若函数 $\text{[math]}$ （ $\text{[math]}$ 为常数）存在两条均过原点的切线，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021·渭滨模拟) 棱长为4的正方体密闭容器内有一个半径为1的小球，小球可在正方体容器内任意运动，则其不能到达的空间的体积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题

12. (2020高一上·山东月考) 我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是（）

A . 这11天复工指数和复产指数均逐日增加； B . 这11天期间，复产指数增量大于复工指数的增量； C . 第3天至第11天复工复产指数均超过80%； D . 第9天至第11天复产指数增量大于复工指数的增量；

答案解析收藏纠错 + 选题

三、填空题

13. (2021·河南模拟) 已知 $\text{[math]}$ 则 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题
14. (2021·河南模拟) 函数 $\text{[math]}$ 的最大值为.

答案解析收藏纠错 + 选题
15. (2021·河南模拟) 已知双曲线 $\text{[math]}$ 的左、右交点分别为 $\text{[math]}$ ，点 $\text{[math]}$ 在双曲线上．若 $\text{[math]}$ 为直角三角形，且 $\text{[math]}$ ，则双曲线的离心率为．

答案解析收藏纠错 + 选题
16. (2021·河南模拟) 在数列 $\text{[math]}$ 中， $\text{[math]}$ ，记 $\text{[math]}$ ，若对任意的 $\text{[math]}$ 恒成立，则实数 $\text{[math]}$ 的取值范围为.

答案解析收藏纠错 + 选题

四、解答题

17. (2021·河南模拟) 在如图所示的空间几何体中，平面 $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 均是等边三角形， $\text{[math]}$ ， $\text{[math]}$ 和平面 $\text{[math]}$ 所成的角为 $\text{[math]}$ ，且点 $\text{[math]}$ 在平面 $\text{[math]}$ 上的射影落在 $\text{[math]}$ 的平分线上.
1. （1）求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值.
答案解析收藏纠错 + 选题
18. (2021·河南模拟) 在① $\text{[math]}$ ，② $\text{[math]}$ 这两个条件中任选一个作为已知条件，补充到下面的横线上并作答.
问题： $\text{[math]}$ 的内角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，已知 .
1. （1）求 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ ，求 $\text{[math]}$ 的面积的最大值.
答案解析收藏纠错 + 选题

19. (2021·河南模拟) 直播带货是扶贫助农的一种新模式，这种模式是利用主流媒体的公信力，聚合销售主播的力量助力打通农产品产销链条，切实助力贫困地区农民脱贫增收．某贫困地区有统计数据显示，2020年该地利用网络直播形式销售农产品的销售主播年龄等级分布如图1所示，一周内使用直播销售的频率分布扇形图如图2所示．若将销售主播按照年龄分为“年轻人”（20岁~39岁）和“非年轻人”（19岁及以下或者40岁及以上）两类，将一周内使用的次数为6次或6次以上的称为“经常使用直播销售用户”，使用次数为5次或不足5次的称为“不常使用直播销售用户”，则“经常使用直播销售用户”中有 $\text{[math]}$ 是“年轻人”．

参考数据：独立性检验临界值表

$\text{[math]}$	0.15	0.10	0.050	0.025	0.010
$\text{[math]}$	2.072	2.706	30841	5.024	6.635

其中， $\text{[math]}$ ．

（1）现对该地相关居民进行“经常使用网络直播销售与年龄关系”的调查，采用随机抽样的方法，抽取一个容量为200的样本，请你根据图表中的数据，完成 $\text{[math]}$ 列联表，并根据列联表判断是否有85%的把握认为经常使用网络直播销售与年龄有关？

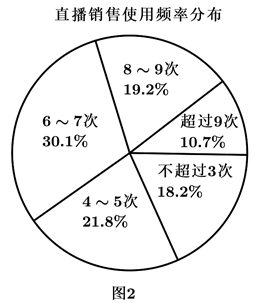
使用直播销售情况与年龄列联表

	年轻人	非年轻人	合计
经常使用直播销售用户
不常使用直播销售用户
合计

（2）某投资公司在2021年年初准备将1000万元投资到“销售该地区农产品”的项目上，现有两种销售方案供选择：
方案一：线下销售．根据市场调研，利用传统的线下销售，到年底可能获利30%，可能亏损15%，也可能不赔不赚，且这三种情况发生的概率分别为 $\text{[math]}$ ；

方案二：线上直播销售．根据市场调研，利用线上直播销售，到年底可能获利50%，可能亏损30%，也可能不赔不赚，且这三种情况发生的概率分别为 $\text{[math]}$ ．

针对以上两种销售方案，请你从期望和方差的角度为投资公司选择一个合理的方案，并说明理由．

答案解析收藏纠错 + 选题

20. (2021·河南模拟) 已知椭圆 $\text{[math]}$ ，直线 $\text{[math]}$ ，直线 $\text{[math]}$ 与椭圆 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ 为坐标原点．
1. （1）若 $\text{[math]}$ ，且 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点，求椭圆 $\text{[math]}$ 的离心率；
2. （2）若椭圆长轴的一个端点为 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于 $\text{[math]}$ 两点，当 $\text{[math]}$ 时，求椭圆 $\text{[math]}$ 的方程．
答案解析收藏纠错 + 选题
21. (2021·河南模拟) 已知函数 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，讨论函数 $\text{[math]}$ 的单调性；
2. （2）当 $\text{[math]}$ 时，关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 有解，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
22. (2021·河南模拟) 在直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 的参数方程为 $\text{[math]}$ （ $\text{[math]}$ 为参数 $\text{[math]}$ ）．以坐标原点 $\text{[math]}$ 为极点， $\text{[math]}$ 轴的正半轴为极轴建立极坐标系，半圆 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ ．
1. （1）求半圆 $\text{[math]}$ 的参数方程和直线 $\text{[math]}$ 的直角坐标方程；
2. （2）直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在半圆 $\text{[math]}$ 上，且直线 $\text{[math]}$ 的倾斜角是直线 $\text{[math]}$ 的倾斜角的2倍， $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2021·河南模拟) 已知 $\text{[math]}$ 是正实数，且满足 $\text{[math]}$ ．
1. （1）是否存在满足已知条件的 $\text{[math]}$ ，使得 $\text{[math]}$ ，试说明理由；
2. （2）求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题