江西省吉安市吉水县2020-2021学年八年级上学期数学期末...

更新时间：2024-07-13 浏览次数：182 类型：期末考试

一、单选题

1. (2020八上·吉水期末) 在直角坐标中，点P（2，﹣3）所在的象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
2. (2020八上·吉水期末) 实数 $\text{[math]}$ ，0，﹣π， $\text{[math]}$ ， $\text{[math]}$ 中无理数的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
3. (2020八上·吉水期末) 下列命题中，是假命题的是（）

A . 两直线平行，则同位角相等 B . 同旁内角互补，则两直线平行 C . 三角形内角和为180° D . 三角形一个外角大于任何一个内角

答案解析收藏纠错 + 选题
4. (2020八上·吉水期末) 有一道题目：已知一次函数y=2x+b，其中b＜0，…，与这段描述相符的函数图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024八上·肃州期末) 下列数据中不能作为直角三角形的三边长是（）

A . 1、1、 $\text{[math]}$ B . 5、12、13 C . 3、5、7 D . 6、8、10

答案解析收藏纠错 + 选题
6. (2021七下·三江期中) 如图，下列条件不能判断直线a∥b的是（）

A . ∠1=∠4 B . ∠3=∠5 C . ∠2+∠5=180° D . ∠2+∠4=180°

答案解析收藏纠错 + 选题

二、填空题

7. (2024九下·长春模拟) 计算： $\text{[math]}$ =

答案解析收藏纠错 + 选题
8. (2020八上·吉水期末) 甲、乙两名同学投掷实心球，每人投10次，平均成绩为7米，方差分别为； S_甲²＝0.1，S_乙²＝0.04，成绩比较稳定的是．

答案解析收藏纠错 + 选题
9. (2020八上·吉水期末) 写出二元一次方程x+4y＝11的一个整数解．

答案解析收藏纠错 + 选题
10. (2020八上·柳州期中) 将一副三角板，按如图方式叠放，那么 $\text{[math]}$ 的度数是．

答案解析收藏纠错 + 选题
11. (2020八下·南县期末) 如图，已知直线y＝ax+b和直线y＝kx交于点P，则关于x，y的二元一次方程组 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
12. (2020八上·吉水期末) 如图，已知一次函数y＝﹣x+1的图象与x轴、y轴分别交于点A ， B ，点M在y轴上（M不与原点重合），并且使以点A ， B ， M为顶点的三角形是等腰三角形，则M的坐标为．

答案解析收藏纠错 + 选题
13. (2020七下·淮滨期中) x﹣2的平方根是±2，2x+y+7的立方根是3，求x²+y²的平方根．

答案解析收藏纠错 + 选题

三、解答题

14. (2020八上·吉水期末)
1. （1）计算： $\text{[math]}$ ；
2. （2）解方程组： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
15. (2024八上·那曲期末) 已知y+1与x﹣1成正比，且当x＝3时y＝﹣5，请求出y关于x的函数表达式，并求出当y＝5时x的值．

答案解析收藏纠错 + 选题
16. (2020八上·吉水期末) 已知在平面直角坐标系中
1. （1）画出△ABC关于x轴成轴对称图形的三角形A′B′C′；
2. （2）写出A′，B′，C′的坐标．
答案解析收藏纠错 + 选题
17. (2020七下·莘县期末) 如图，已知：CF⊥AB于F，ED⊥AB于D，∠1＝∠2，求证：FG∥BC.

答案解析收藏纠错 + 选题
18. (2023八上·达州期末) 我市为加快美丽乡村建设，建设秀美幸福抚州，对A、B两类村庄进行了全面改建．根据预算，建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元；甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元．
1. （1）建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元？
2. （2）乙镇3个A类美丽村庄和4个B类村庄改建共需资金多少万元？
答案解析收藏纠错 + 选题
19. (2020八上·吉水期末) 某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型， $\text{[math]}$ ：4棵； $\text{[math]}$ ：5棵； $\text{[math]}$ ：6棵； $\text{[math]}$ ：7棵；将各类的人数绘制成扇形图（如图1）和条形图（如图2）.回答下列问题：
1. （1）在这次调查中D类型有多少名学生？（并在图中画出）
2. （2）写出被调查学生每人植树量的众数、中位数；
3. （3）求被调查学生每人植树量的平均数，并估计这260名学生共植树多少棵？
答案解析收藏纠错 + 选题
20. (2021八下·阳谷期末) 如图，在四边形ABCD中，CD＝AD＝ $\text{[math]}$ ，∠D＝90°，AB＝5．BC＝3．
1. （1）求∠C的度数；
2. （2）求四边形ABCD的面积．
答案解析收藏纠错 + 选题
21. (2021八下·黟县期末) 阅读下列一段文字，然后回答下列问题．
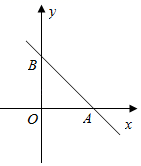
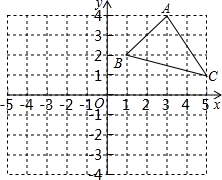
已知平面内两点 M（x1，y1）、N（x2，y2），则这两点间的距离可用下列公式计算： MN= $\text{[math]}$ ．

例如：已知 P（3，1）、Q（1，﹣2），则这两点间的距离 PQ= $\text{[math]}$ = $\text{[math]}$ ．

特别地，如果两点 M（x1，y1）、N（x2，y2）所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴，那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨．
1. （1）已知 A（1，2）、B（﹣2，﹣3），试求 A、B 两点间的距离；
2. （2）已知 A、B 在平行于 x 轴的同一条直线上，点 A 的横坐标为 5，点 B 的横坐标为﹣1，
  试求 A、B 两点间的距离；
3. （3）已知△ABC 的顶点坐标分别为 A（0，4）、B（﹣1，2）、C（4，2），你能判定△ABC 的形状吗？请说明理由．
答案解析收藏纠错 + 选题
22. (2024七下·南昌期中) 如图，∠ADE+∠BCF＝180°，BE平分∠ABC，∠ABC＝2∠E．
1. （1） AD与BC平行吗？请说明理由；
2. （2） AB与EF的位置关系如何？为什么？
3. （3）若AF平分∠BAD，试说明：∠E+∠F＝90°
答案解析收藏纠错 + 选题
23. (2021八下·固阳期末) 如图，直线l：y＝﹣ $\text{[math]}$ x+2与x轴，y轴分别交于A，B两点，在y轴上有一点C（0，4），动点M从点A出发以每秒1个单位的速度沿x轴向左移动．
1. （1）求A，B两点的坐标；
2. （2）求△COM的面积S与点M的移动时间t之间的函数关系式；
3. （3）当t＝6时，
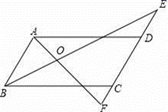
  ①直接写出直线CM所对应的函数表达式；
  
  ②问直线CM与直线 $\text{[math]}$ 有怎样的位置关系？请说明理由．
答案解析收藏纠错 + 选题