江西省抚州市2020-2021学年九年级上学期数学期末试卷

更新时间：2021-04-23 浏览次数：156 类型：期末考试

一、单选题

1. (2023九上·奉贤期中) 下列线段中，能成比例的是（）

A . 3cm、6cm、8cm、9cm B . 3cm、5cm、6cm、9cm C . 3cm、6cm、7cm、9cm D . 3cm、6cm、9cm、18cm

答案解析收藏纠错 + 选题
2. (2020九上·抚州期末) 如图是某体育馆内的颁奖台，其主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020九上·抚州期末) 已知反比例函数y＝ $\text{[math]}$ ，下列结论中错误的是（）

A . 图象经过点（﹣1，﹣1） B . 当x＜0时，y随着x的增大而增大 C . 当x＞1时，0＜y＜1 D . 图象在第一、三象限

答案解析收藏纠错 + 选题
4. (2020九上·砚山期末) 将抛物线 $\text{[math]}$ 先向左平移1个单位长度，再向上平移2个单位长度，所得抛物线的解析式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·抚州期末) 一元二次方程x²﹣3x+1＝0的两个根为x₁ ， x₂ ，则x₁²+3x₂+x₁x₂+1的值为（）

A . 10 B . 9 C . 8 D . 7

答案解析收藏纠错 + 选题
6. (2020九上·抚州期末) 已知二次函数 $\text{[math]}$ 的图象如图所示，有下列4个结论：

① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤2c<3b

其中正确的结论有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

二、填空题

7. (2021九上·廉江期末) 抛物线y＝（x+2）²+1的顶点坐标为．

答案解析收藏纠错 + 选题
8. (2020九上·抚州期末) 如图，体育兴趣小组选一名身高1.6m的同学直立于旗杆影子的顶端处，其他人分为两部分，一部分同学测得该同学的影长为1.2m，另一部分同学测得同一时刻旗杆影长为9m，那么旗杆的高度是m．

答案解析收藏纠错 + 选题
9. (2020九上·抚州期末) 若 $\text{[math]}$ ，那么△ABC的形状是．

答案解析收藏纠错 + 选题
10. (2020九上·抚州期末) 如图，在边长为1的小正方形网格中，点A ， B ， C ， D都在这些小正方形的顶点上，AB ， CD相交于点O ，则cos∠BOD＝．

答案解析收藏纠错 + 选题
11. (2020九上·抚州期末) 如图，在▱ABCD中，对角线AC ， BD相交于点O ，在DC的延长线上取一点E ，使CE＝ $\text{[math]}$ CD ，连接OE交BC于点F ，若BC＝4，则CF＝．

答案解析收藏纠错 + 选题
12. (2023九上·宝安开学考) 如图， $\text{[math]}$ ， $\text{[math]}$ ， AB=6，CD=4，BD=14.点P在BD上移动，当以P ， C ， D为顶点的三角形与△ABP相似时，则PB的长为．

答案解析收藏纠错 + 选题

三、解答题

13. (2020九上·抚州期末)
1. （1）解方程： $\text{[math]}$ ；
2. （2）计算： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
14. (2020九上·抚州期末) 已知 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个根，求方程的另一个根及c的值.

答案解析收藏纠错 + 选题
15. (2020九上·抚州期末) 如图，是由两个等边三角形和一个正方形拼在-起的图形，请仅用无刻度的直尺按要求画图，
1. （1）在图①中画一个 $\text{[math]}$ 的角，使点 $\text{[math]}$ 或点 $\text{[math]}$ 是这个角的顶点，且以 $\text{[math]}$ 为这个角的一边：
2. （2）在图②画一条直线 $\text{[math]}$ ，使得 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
16. (2021九上·普宁期末) 江西两所医院分别有一男一女共4名医护人员支援湖北随州抗击疫情．
1. （1）若从甲、乙两医院支援的医护人员中分别随机选1名，则所选的2名医护人员性别相同的概率是．
2. （2）若从支援的4名医护人员中随机选2名，用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率．
答案解析收藏纠错 + 选题
17. (2020九上·抚州期末) 如图，把一张矩形纸片沿对角线折叠．
1. （1）重合部分是什么图形？请说明理由．
2. （2）若AB＝4，BC＝8，求△BDF的面积．
答案解析收藏纠错 + 选题
18. (2021九上·安庆月考) 已知：二次函数y＝ax²+bx+c（a≠0）中的x和y满足表：

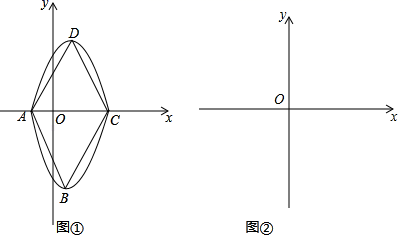
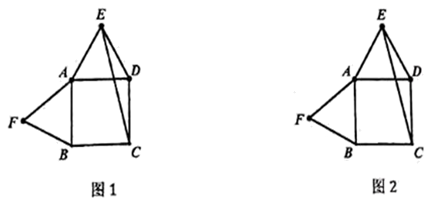
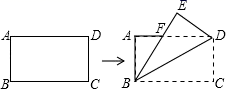
x

…

﹣1

0

1

2

3

…

y

…

3

0

﹣1

0

m

…
1. （1）观察表可求得m的值为；
2. （2）请求出这个二次函数的表达式．
答案解析收藏纠错 + 选题

19. (2020九上·抚州期末) 阳光市场某个体商户购进某种电子产品，每个进价50元．调查发现，当售价为80元时，平均一周可卖出160个，而当每售价每降低2元时，平均一周可多卖出20个．若设每个电子产品降价x元，

（1）根据题意，填表：

	进价（元）	售价（元）	每件利润（元）	销量（个）	总利润（元）
降价前	50	80	30	160	$\text{[math]}$
降价后	50

（2）若商户计划每周盈利5200元，且尽量减少库存，则每个电子产品应降价多少元？

答案解析收藏纠错 + 选题

20. (2020九上·抚州期末) 为倡导“绿色出行，低碳生活”的号召，今年春天，安庆市的街头出现了一道道绿色的风景线－－“共享单车”. 图（1）所示的是一辆共享单车的实物图. 图（2）是这辆共享单车的部分几何示意图，其中车架档AC长为40cm，座杆CE的长为18cm. 点A、C、E在同一条直线上，且∠CAB=60°，∠ACB=75°
1. （1）求车座点E到车架档AB的距离；
2. （2）求车架档AB的长.
答案解析收藏纠错 + 选题
21. (2020九上·抚州期末) 已知正比例函数y₁＝ax的图象与反比例函数y₂＝ $\text{[math]}$ 的图象交于A ， B两点，且A点的横坐标为﹣1．
1. （1）试确定上述正比例函数和反比例函数的表达式．
2. （2）根据图象回答，当x取何值时，反比例函数的值大于正比例函数的值．
3. （3）点M（m ， n）是反比例函数图象上一动点，其中0＜n＜3，过点M作MD∥y轴交x轴于点D ，过点B作BC∥x轴交y轴于点C ，交直线MD于点E ，当四边形OMEB面积为3时，请判断DM与EM大小关系并给予证明．
答案解析收藏纠错 + 选题
22. (2020九上·抚州期末) 如图

如图1，把两个相似比为 $\text{[math]}$ 的矩形ABCD与矩形CEFG拼成如图所示的图案．
1. （1）（一）问题发现：
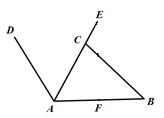
  请探究AC与CF的位置关系并证明．
2. （2）求 $\text{[math]}$ 的值．
3. （3）（二）拓展应用：
  如图2，在四边形ABCF中，已知∠ABC＝90°，AB＝3，BC＝4，CF＝10，AF＝5 $\text{[math]}$ ．
  
  求tan∠AFC；
4. （4）连接BF ，求BF的长．
答案解析收藏纠错 + 选题
23. (2020九上·抚州期末) 定义：在平面直角坐标系中，抛物线y＝a $\text{[math]}$ +bx+c（a≠0）与直线y＝m交于点A、C（点C在点A右边）将抛物线y＝a $\text{[math]}$ +bx+c沿直线y＝m翻折，翻折前后两抛物线的顶点分别为点B、D．我们将两抛物线之间形成的封闭图形称为惊喜线，四边形ABCD称为惊喜四边形，对角线BD与AC之比称为惊喜度（Degreeofsurprise），记作|D|＝ $\text{[math]}$ ．
1. （1）图①是抛物线y＝ $\text{[math]}$ ﹣2x﹣3沿直线y＝0翻折后得到惊喜线．则点A坐标，点B坐标，惊喜四边形ABCD属于所学过的哪种特殊平行四边形，|D|为．
2. （2）如果抛物线y＝m $\text{[math]}$ ﹣6m（m＞0）沿直线y＝m翻折后所得惊喜线的惊喜度为1，求m的值．
3. （3）如果抛物线y＝ $\text{[math]}$ ﹣6m沿直线y＝m翻折后所得的惊喜线在m﹣1≤x≤m+3时，其最高点的纵坐标为16，求m的值并直接写出惊喜度|D|．
答案解析收藏纠错 + 选题