
 B .
B .  C .
C .  D .
D . 
| 日期 | 一 | 二 | 三 | 四 | 五 | 方差 | 平均气温 |
| 最低气温 | 1℃ | ﹣1℃ | 2℃ | 0℃ | ■ | ■ | 1℃ |

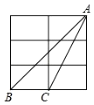





请解答下列问题:

|
销售时段 |
销售数量 |
销售利润 |
|
|
A型 |
B型 |
||
|
第一周 |
3台 |
5台 |
1800元 |
|
第二周 |
4台 |
10台 |
3000元 |
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?

①若CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限,当线段PQ= AB时,求∠CED的正切值;
②若点G是直线x=1上一点,当△CEG与△AOC相似时,请直接写出点E的坐标.

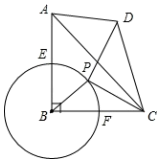
①求证:EN=GN;
②连接OC,求证:△CHO≌△HEN.