湖北省鄂州市梁子湖区2017年中考数学模拟试卷（5月份

更新时间：2017-11-08 浏览次数：1040 类型：中考模拟

一、选择题

1. (2017·梁子湖模拟) ﹣5的倒数是（）

A . ﹣5 B . $\text{[math]}$ C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
2. (2017·梁子湖模拟) 下列运算正确的是（）

A . 2a³÷a=6 B . （a+b）（a﹣b）=a²﹣b² C . （ab³）²=a²b⁵ D . （a+b）²=a²+b²

答案解析收藏纠错 + 选题
3. (2023七上·东莞期末) 节约是一种美德，节约是一种智慧．据不完全统计，全国每年浪费食物总量折合粮食可养活约3亿5千万人.350 000 000用科学记数法表示为（）

A . 3.5×10⁷ B . 3.5×10⁸ C . 3.5×10⁹ D . 3.5×10¹⁰

答案解析收藏纠错 + 选题
4. (2017·梁子湖模拟) 由6个大小相同的小正方体组合成一个几何体，其俯视图如图所示，其中正方形中的数字表示该位置放置的小正方体的个数，则该几何体的左视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2017·梁子湖模拟) 下列说法不正确的是（）

A . 调查一架“歼20”隐形战机各零部件的质量，应采用抽样调查 B . 一组数据2，2，3，3，3，4的众数是3 C . 如果x₁与x₂的平均数是4，那么x₁+1与x₂+5的平均数是7 D . 一组数据1，2，3，4，5的方差是2，那么数据11，12，13，14，15的方差也是2

答案解析收藏纠错 + 选题
6. (2017·梁子湖模拟) 如图，AB∥CD，∠CDE=130°，则∠A的度数是（）

A . 130° B . 50° C . 70° D . 30°

答案解析收藏纠错 + 选题
7. (2017·梁子湖模拟) 如图，一次函数y=kx+b与反比例函数y= $\text{[math]}$ （x＞0）的图象交于A（m，6），B（3，n）两点，与x轴交于点C，与y轴交于点D，下列结论：①一次函数解析式为y=﹣2x+8；②AD=BC；③kx+b﹣ $\text{[math]}$ ＜0的解集为0＜x＜1或x＞3；④△AOB的面积是8，其中正确结论的个数是（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
8. (2017·梁子湖模拟) 如图，正方形ABCD中，点E，F分别在边CD，BC上，且∠EAF=45°，BD分别交AE，AF于点M，N，以点A为圆心，AB长为半径画弧BD．下列结论：①DE+BF=EF；②BN²+DM²=MN²；③△AMN∽△AFE；④ $\text{[math]}$ 与EF相切；⑤EF∥MN．其中正确结论的个数是（）

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题
9. (2017·梁子湖模拟) 二次函数y=ax²+bx+c（a，b，c为常数，且a≠0）中，x与y的部分对应值如下表：
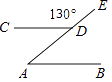
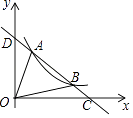
x
﹣3
﹣2
﹣1
0
y
0
﹣3
﹣4
﹣3
下列结论：
①ac＜0；
②当x＞1时，y随x的增大而增大；
③﹣4是方程ax²+（b﹣4）x+c=0的一个根；
④当﹣1＜x＜0时，ax²+（b﹣1）x+c+3＞0．其中正确结论的个数为（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
10. (2017·梁子湖模拟) 如图，正方形ABCD中，AB=4，点E是边BC的中点，点G，H分别是边CD，AB上的动点，连接GH交AE于F，且使GH⊥AE，连接AG，EH，则EH+AG的最小值是（）

A . 8 B . 4 $\text{[math]}$ C . 2 $\text{[math]}$ D . 8 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2017·梁子湖模拟) 把多项式16x³﹣9xy²分解因式的结果是．

答案解析收藏纠错 + 选题
12. (2017·梁子湖模拟) 已知关于x，y的方程组 $\text{[math]}$ 的解满足不等式x+y＞3，则a的取值范围是．

答案解析收藏纠错 + 选题
13. (2017·梁子湖模拟) 如图，在扇形OAB中，∠AOB=90°，半径OA=2 $\text{[math]}$ ，将扇形OAB沿过点B的直线折叠，点O恰好落在 $\text{[math]}$ 上的点D处，折痕交OA于点C，则阴影部分的面积是．

答案解析收藏纠错 + 选题
14. (2017·梁子湖模拟) 如图，某电信公司提供了A，B两种方案的移动通讯费用y（元）与通话时间x（元）之间的关系，下列结论：
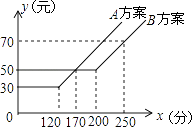
①若通话时间少于120分，则A方案比B方案便宜20元；
②若通话时间超过200分，则B方案比A方案便宜12元；
③若通讯费用为60元，则B方案比A方案的通话时间多；
④若两种方案通讯费用相差10元，则通话时间是145分或185分．其中正确结论的序号是．

答案解析收藏纠错 + 选题
15. (2017·梁子湖模拟) 已知△ABC中，AB=15，AC=13，AD⊥BC于D，AD=12，⊙O是△ABC的外接圆，则⊙O的半径是．

答案解析收藏纠错 + 选题
16. (2017·梁子湖模拟) 已知：如图，在△ABC中，cos∠ABC= $\text{[math]}$ ，sin∠ACB= $\text{[math]}$ ，AC=2，分别以AB，AC为边向△ABC形外作正方形ABGF和正方形ACDE，连接EF，点M是EF的中点，连接AM，则AM的长为．

答案解析收藏纠错 + 选题

三、解答题

17. (2017·梁子湖模拟) 先化简，再求值：
$\text{[math]}$ ÷（ $\text{[math]}$ ﹣x﹣3），其中x=sin45°﹣4cos60°．

答案解析收藏纠错 + 选题
18. (2021八下·广宁期末) 如图，BD是△ABC的角平分线，点E，F分别在BC，AB上，且DE∥AB，BE=AF．
1. （1）求证：四边形ADEF是平行四边形；
2. （2）若∠ABC=60°，BD=4，求平行四边形ADEF的面积．
答案解析收藏纠错 + 选题
19. (2017·梁子湖模拟) 为了贯彻落实国家关于增强青少年体质的计划，鄂州市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程．某牛奶供应商拟提供A（原味）、B（草莓味）、C（核桃味）、D（菠萝味）、E（香橙味）等五种口味的学生奶供学生选择（所有学生奶盒形状、大小相同），为了解对学生奶口味的喜好情况，某初级中学七年级（1）班李老师对全班同学进行了调查统计，制成了如图两幅不完整的统计图．
1. （1）该班五种口味的学生奶的喜好人数组成一组统计数据，直接写出这组数据的平均数，并将折线统计图补充完整．
2. （2）在进行调查统计的第二天，李老师为班上每位同学发放一盒学生奶．喜好A味的小聪和喜好B味的小明等四位同学最后领取，剩余的学生奶放在同一纸箱里，分别有A味2盒，B味和C味各1盒，李老师从该纸箱里随机取出两盒学生奶．请你用列表法或画树状图的方法，求出这两盒牛奶恰好同时是小聪和小明喜好的学生奶的概率．
答案解析收藏纠错 + 选题
20. (2017·梁子湖模拟) 已知二次函数y=a（x﹣m）²﹣a（x﹣m）（a，m为常数，且a≠0）．
1. （1）求证：不论a与m为何值，该函数的图象与x轴总有两个公共点；
2. （2）设该函数的图象与x轴的两个交点为A（x₁ ， 0），B（x₂ ， 0），且x₁²+x₂²=25，求m的值；
3. （3）设该函数的图象的顶点为C，与x轴交于A，B两点，且△ABC的面积为1，求a的值．
答案解析收藏纠错 + 选题
21. (2018·南湖模拟) 一幢房屋的侧面外墙壁的形状如图所示，它由等腰三角形OCD和矩形ABCD组成，∠OCD=25°，外墙壁上用涂料涂成颜色相同的条纹，其中一块的形状是四边形EFGH，测得FG∥EH，GH=2.6m，∠FGB=65°．
1. （1）求证：GF⊥OC；
2. （2）求EF的长（结果精确到0.1m）．
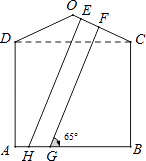
  （参考数据：sin25°=cos65°≈0.42，cos25°=sin65°≈0.91）
答案解析收藏纠错 + 选题
22. (2017·梁子湖模拟) 如图，AB是⊙O的直径，点C为AB上一点，作CD⊥AB交⊙O于D，连接AD，将△ACD沿AD翻折至△AC′D．
1. （1）请你判断C′D与⊙O的位置关系，并说明理由；
2. （2）过点B作BB′⊥C′D′于B′，交⊙O于E，若CD= $\text{[math]}$ ，AC=3，求BE的长．
答案解析收藏纠错 + 选题
23. (2017·梁子湖模拟) 为积极支持鄂州市创建国家卫生城市工作，某商家计划从厂家采购A，B两种清洁产品共20件，产品的采购单价（元/件）是采购数量（件）的相关信息如下表所示．
采购数量（件）
2
4
6
…
A产品单价（元）
1460
1420
1380
…
B产品单价（元）
1280
1260
1240
…
1. （1）设B产品的采购数量为x（件），采购单价为y₁（元/件），求y₁与x的关系式；
2. （2）经商家与厂家协商，采购A产品的数量不少于B产品数量的 $\text{[math]}$ ，且B产品采购单价不高于1250元，求该商家共有几种进货方案？
3. （3）该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大？并求最大利润．
答案解析收藏纠错 + 选题
24. (2017·梁子湖模拟) 如图，在平面直角坐标系中，已知A（﹣2，0），C（0，4），点O′为x轴上一点，⊙O′过A，C两点交x轴于另一点B．
1. （1）求点O′的坐标；
2. （2）已知抛物线y=ax²+bx+c过A，B，C三点，且与⊙O′交于另一点E，求抛物线的解析式，并直接写出点E 坐标；
3. （3）设点P（t，0）是线段OB上一个动点，过点P作直线l⊥x轴，交线段BC于F，交抛物线y=ax²+bx+c于点G，请用t表示四边形BPCG的面积S；
4. （4）在（3）的条件下，四边形BPCG能否为平行四边形？若能，请求出t的值；若不能，请说明理由．
答案解析收藏纠错 + 选题