初中数学北师大版七年级下学期第四章 4.5 利用三角形全等...

更新时间：2021-04-13 浏览次数：134 类型：同步测试

一、单选题

1. (2020八上·台安月考) 要测量河两岸相对的两点 $\text{[math]}$ ， $\text{[math]}$ 的距离，先在 $\text{[math]}$ 的垂线 $\text{[math]}$ 上取两点 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ，再作出 $\text{[math]}$ 的垂线 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在一条直线上（如图），可以说明 $\text{[math]}$ ，得 $\text{[math]}$ ，因此测得 $\text{[math]}$ 的长就是 $\text{[math]}$ 的长.判定 $\text{[math]}$ 最恰当的理由是（）

A . 边角边 B . 角边角 C . 边边边 D . 斜边、直角边

答案解析收藏纠错 + 选题
2. (2021七下·崂山期末) 在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝a，EF＝b，圆形容器的壁厚是（）

A . a B . b C . b﹣a D . $\text{[math]}$ （b﹣a）

答案解析收藏纠错 + 选题
3. (2020七上·蓬莱期末) 某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事方法是（）

A . 带①去 B . 带②去 C . 带③去 D . ①②③都带去

答案解析收藏纠错 + 选题
4. (2023八上·越城月考) 如图小敏做了一个角平分仪ABCD，其中AB= AD，BC= DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD ，使它们分别落在角的两边上，过点A、C画一条射线AE，AE就是∠PRQ的平分线。此角平分仪的画图原理是（）

A . SSS B . SAS C . ASA D . AAS

答案解析收藏纠错 + 选题
5. (2021八上·崆峒期末) 如图，A，B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长，位同学帮他想了一个主意：先在地上取一个可以直接到达A，B的点C，连接AC并延长到点D，使 $\text{[math]}$ ，连接BC并延长到点E，使 $\text{[math]}$ ，连接DE并且测出DE的长即为A，B间的距离，这样实际上可以得到 $\text{[math]}$ ，理由是（）

A . SSS B . AAS C . ASA D . SAS

答案解析收藏纠错 + 选题
6. (2020八上·上思月考) 装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块（如图所示），他要拿哪一块回公司才能更换到相匹配的陶瓷片（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题

二、填空题

7. (2020八上·农安月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E，F是AD上的任意两点、若 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
8. (2023八上·浦北期中) 如图所示，要测量河两岸相对的两点A、B的距离，在AB的垂线BF上取两点C、D，使BC=CD，过D作BF的垂线DE，与AC的延长线交于点E，若测得DE的长为25米，则河宽AB长为．

答案解析收藏纠错 + 选题
9. (2020七下·清涧期末) 如图，把两根钢条 $\text{[math]}$ ， $\text{[math]}$ 的中点连在一起做成卡钳，可测量工件内槽的宽，已知 $\text{[math]}$ 的长度是 $\text{[math]}$ ，则工件内槽的宽 $\text{[math]}$ 是cm．

答案解析收藏纠错 + 选题
10. (2020八上·长汀月考) 如图，AB=12，CA⊥AB于A，DB⊥AB于B，且AC=4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动分钟后△CAP与△PQB全等.

答案解析收藏纠错 + 选题
11. (2020八上·北京期中) 如图，要测量池塘两岸相对的两点A ， B的距离，可以在池塘外取AB的垂线BF上的两点C ， D ，使BC=CD ，再画出BF的垂线DE ，使E与A ， C在一条直线上.若想知道两点A ， B的距离，只需要测量出线段即可．

答案解析收藏纠错 + 选题
12. (2019八上·长兴月考) 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)．你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第块。依据。

答案解析收藏纠错 + 选题

三、解答题

13. 如图，工人师傅要检查人字梁的∠B和∠C是否相等，但他手边没有量角器，只有一个刻度尺．他是这样操作的：①分别在BA和CA上取BE＝CG；②在BC上取BD＝CF；③量出DE的长为a m，FG的长为b m．如果a＝b，则说明∠B和∠C是相等的，他的这种做法合理吗？为什么？

答案解析收藏纠错 + 选题
14. (2021八上·施秉期末) 如图所示，C、D分别位于路段A、B两点的正北处与正南处，现有两车分别从E、F两处出发，以相同的速度直线行驶，相同时间后分别到达C、D两地，休整一段时间后又以原来的速度直线行驶，最终同时到达A、B两点，那么CE与DF平行吗？为什么？

答案解析收藏纠错 + 选题
15. (2021八上·北海期末) 某中学八年级同学到野外开展数学综合实践活动，在营地看到一池塘，同学们想知道池塘两端的距离.某同学设计了如下测量方案：先取一个可直接到达池塘的两端的点 $\text{[math]}$ ， $\text{[math]}$ 的点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，分别延长 $\text{[math]}$ 至点 $\text{[math]}$ ， $\text{[math]}$ 至点 $\text{[math]}$ ，使得 $\text{[math]}$ ， $\text{[math]}$ .再测出 $\text{[math]}$ 的长度即可知道 $\text{[math]}$ 之间的距离.他的方案可行吗？请说明理由.

答案解析收藏纠错 + 选题
16. (2020七下·陈仓期末) 如图，一根电线杆 $\text{[math]}$ 直立在水平地面上的点 $\text{[math]}$ 处，分别用钢丝绳 $\text{[math]}$ ， $\text{[math]}$ 将它加固，两根钢丝绳分别固定在地面上的点 $\text{[math]}$ 处，点 $\text{[math]}$ 在同一条直线上，小明测得 $\text{[math]}$ ，两根钢丝绳相等吗？请说明理由.

答案解析收藏纠错 + 选题
17. (2019八上·天台月考) 仅用一块没有刻度的直角三角板能画出图1∠AOB的平分线吗?
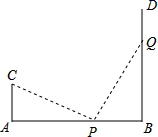
小刚想出了这样的方法：如图2所示，先将直角三角板的一个锐角顶点和∠AOB的顶点O重合，一条直角边与OA重叠(重叠部分为OC)，沿另一条直角边画出直线m；再将三角板的同一锐角顶点与O重合，同一条直角边与OB重叠(重叠部分为OD)，沿另一条直角边画山直线n，m与n交于点P，连接OP并延长，则射线OP为∠AOB的平分线，你认为小刚的方法正确吗?为什么?

答案解析收藏纠错 + 选题
18. (2020八上·万山期中)
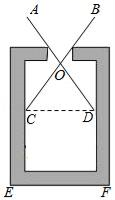
你一定玩过跷跷板吧！如图是小明和小刚玩跷跷板的示意图，横板绕它的中点O上下转动，立柱OC与地面垂直．当一方着地时，另一方上升到最高点．问：在上下转动横板的过程中，两人上升的最大高度AA′、BB′有何数量关系，为什么？

答案解析收藏纠错 + 选题