


|
平方根 |
立方根 |
|
|
定义 |
一般地,如果一个数x的平方等于a,即 | 一般地,如果一个数x的立方等于a,即 |
| 运算 | 求一个数a的平方根的运算叫做开平方.开平方和平方互为逆运算. | 求一个数a的立方根的运算叫做开立方.开立方和立方互为逆运算 |
| 性质 | 一个正数有两个平方根,它们互为相反数:0的平方根是0;负数没有平方根. | 正数的立方根是正数;0的立方根是0;负数的立方根是负数. |
| 表示方法 | 正数a的平方根可以表示为“ | 一个数a的立方根可以表示为“ |
今天我们类比平方根和立方根的学习方法学习四次方根.
(类比探索)
|
| | | |
| |
|
|
|
类比平方根和立方根,给四次方根下定义:
.
① 的四次方根是;②
的四次方根是;
③ 的四次方根是;④
的四次方根是;
⑤ 的四次方根是;⑥
(填“有"或"“没有”)四次方根.
类比平方根和立方根的性质,归纳四次方根的性质:
;
(拓展应用)
① ;
② ;
③比较大小:
.

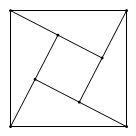
如图 ,在四边形
中,
,
,
.点E,F分别是
和
上的点,且
,试探究线段
,
,
之间的关系.小明同学探究此问题的方法是:延长
到点G,使
,连接
.先证明
,再证明
,进而得出
.你认为他的做法;(填“正确”或“错误”).

如图 ,在四边形
中,
,
,
,
,点E,F分别是
和
上的点,且
,上题中的结论依然成立吗?请说明理由.

小明通过对前面两题的认真思考后得出:如图 ,在四边形
中,若
,
,
,那么
.你认为符合题意吗?请说明理由.
