 B .
B .  C .
C .  D .
D . 
| 日期 | 收入(+)或支出(﹣) | 结余 | 注释 |
| 2日 | 3.5 | 8.5 | 卖废品 |
| 3日 | ﹣4.5 | 4.0 | 买圆珠笔、铅笔芯 |
| 4日 | ■ | ﹣1.2 | 买科普书,同学代付 |
但由保存不当,“4日”的收入或支出被墨水涂污了,请你算出“4日”的收入或支出以及“1日”的结余,分别是( )
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

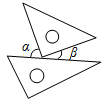 B .
B .  C .
C . 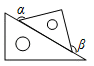 D .
D . 

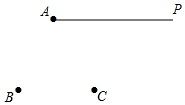
⑴画射线AB;
⑵用尺规在射线AP上截取AD=AB;
⑶连接BC , 并延长BC到E , 使CE=2BC .
|
星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
|
跑步情况 |
+460 |
+220 |
﹣250 |
﹣10 |
﹣330 |
+50 |
+560 |