江苏省盐城市2021届九年级下学期数学期中考试试卷

更新时间：2021-07-10 浏览次数：224 类型：期中考试

一、单选题

1. (2021九下·盐城期中) －2021的绝对值是（）

A . 2021 B . $\text{[math]}$ C . - $\text{[math]}$ D . -2021

答案解析收藏纠错 + 选题
2. (2021九下·盐城期中) 下列运算正确的是（）

A . x²·x³=x6 B . x²+x²=2x⁴ C . （－3a³）·（－5a⁵）=15a⁸ D . （－2x）²=－4x²

答案解析收藏纠错 + 选题
3. (2021九下·盐城期中) 人间四月芳菲始，踏青赏花正当时．记者从市文广旅局了解到，2021年清明小长假，我市统计的重点景区共接待游客186.5万人次，把186.5万用科学记数法表示为（）

A . 1.865×10⁸ B . 1.865×10⁷ C . 1.865×10⁶ D . 1.865×10²

答案解析收藏纠错 + 选题
4. (2021九下·盐城期中) 如图，直线a // b，点B在直线b上，且AB⊥BC，∠2＝65°，则∠1的度数为（）

A . 65° B . 45° C . 35° D . 25°

答案解析收藏纠错 + 选题
5. (2023九下·柯桥月考) 下列四个立体图形中，从正面看到的图形与其他三个不同的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2021九下·盐城期中) 某车间3月下旬生产零件的次品数如下（单位：个）：0，2，0，2，3，0，2，3，1，2，则在这10天中该车间生产的零件的次品数的（）

A . 众数是0 B . 中位数是2 C . 平均数是2 D . 极差是2

答案解析收藏纠错 + 选题
7. (2021九下·盐城期中) 若⊙O半径是2，点A在直线l上，且OA=2，则直线l与⊙O的位置关系是（）

A . 相切 B . 相交 C . 相离 D . 相切或相交

答案解析收藏纠错 + 选题
8. (2021九下·盐城期中) 如图，已知△ABC是等腰直角三角形，∠ABC=90°，A点坐标（－2，0），B点坐标为（1，1），点C在反比例函数 $\text{[math]}$ 上，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . -4 D . -2

答案解析收藏纠错 + 选题

二、填空题

9. (2021九下·盐城期中) 若二次根式 $\text{[math]}$ 有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
10. 分解因式： $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021九下·盐城期中) 一个正多边形的每个外角为30°，则这个正多边形的边数为．

答案解析收藏纠错 + 选题
12. (2021九下·盐城期中) 在一次跳远训练中，甲、乙两人每人5次跳远的平均成绩都是2.38米，方差分别是 $\text{[math]}$ （米2）， $\text{[math]}$ （米2），则在这次跳远训练中成绩比较稳定的是．

答案解析收藏纠错 + 选题
13. (2021九下·盐城期中) 已知实数m是关于x的方程 $\text{[math]}$ -3x-1=0的一根，则代数式2 $\text{[math]}$ -6m+2值为．

答案解析收藏纠错 + 选题
14. (2021九下·盐城期中) 如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹为120°，AB长为25cm，则纸扇外边缘弧BC长为cm．

答案解析收藏纠错 + 选题
15. (2021九下·盐城期中) 如图为甲、乙、丙三根笔直的钢管平行摆放在地面上的情形．已知乙有一部分只与甲重叠，其余部分只与丙重叠，甲没有与乙重叠的部分的长度为2m，丙没有与乙重叠的部分的长度为3m．若乙的长度最长且甲、乙的长度相差xm，乙、丙的长度相差ym，则乙的长度为m(用含有x、y的代数式表示)．

答案解析收藏纠错 + 选题
16. (2021九下·盐城期中) 某园林单位要在一个绿化带内开挖一个△ABC的工作面，使得∠ACB=60°，CD是AB边上的高，且CD=6，则△ABC的面积最小值是．

答案解析收藏纠错 + 选题

三、解答题

17. (2021九下·盐城期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021九下·盐城期中) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2024八下·新罗月考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2021九下·盐城期中) 已知：在▱ABCD中，E、F是对角线AC上的两点，且AE＝CF，对角线AC、BD交于点O．

求证：
1. （1） △ABF≌△CDE；
2. （2） BF//DE．
答案解析收藏纠错 + 选题
21. (2021九下·盐城期中) 如图，在平面直角坐标系中，直线l1：y＝－x+3与过点A（－3，0）的直线l2交于点P（－1，m），与x轴交于点B．
1. （1）求直线l2的函数表达式；
2. （2）点M在直线l2上，MN//y轴，交直线l1于点N，若MN＝AB，求点M的坐标.
答案解析收藏纠错 + 选题

22. (2021九下·盐城期中) 中国共产党，一个神圣而庄重的名字，今年我们伟大的党已经走过100年的光辉历程．为了庆祝中国共产党诞辰100周年，某校1000名学生准备在2021年7月1日“建党节”期间开展庆祝活动，对表达祝贺的方式，某班兴趣小组随机抽取了部分学生进行问卷调查，并将问卷调查的结果绘制成如下不完整的统计表：

对党诞辰100周年祝贺的方式的统计表

方式	频数	百分比
诗歌朗诵	23	46%
歌唱
舞蹈		8%
其他	15
合计		100%

（1）本次问卷调查抽取的学生共有人，其中通过舞蹈表达祝贺的学生有人．
（2）分析上表的“频数”、“百分比”两列数据，补全扇形统计图横线上缺失的数据．
（3）根据抽样的结果，估计该校学生通过歌唱表达祝贺的约有多少人？

答案解析收藏纠错 + 选题

23. (2021九下·盐城期中) 如图，已知△ABC中，AB＝8，AC＝6．
1. （1）请用直尺（不带刻度）和圆规，按下列要求作图：
  ①作∠CAB的角平分线交BC于点E；②作线段AE的垂直平分线分别交AB、AC于点D、F．
2. （2）连接DE、EF，求四边形ADEF的周长．
答案解析收藏纠错 + 选题
24. (2021·南通模拟) 疫情防控期间，任何人进入校园都必须测量体温，体温正常方可进校．现在学校需在东门、南门和西门分别增加一人测温，甲、乙、丙三人被随机增派到三个校门测温．小明每天走东门进校，小丽每天走西门进校．请用所学概率知识解决下列问题：
1. （1）写出甲、乙、丙被分配到三个校门测温的所有可能结果；
2. （2）小明、小丽两人中，进校时谁遇到甲的可能性大？请说明理由．
答案解析收藏纠错 + 选题
25. (2021九下·盐城期中) 已知：一个⊙O与一个含有30°的Rt△CDE如图摆放，其中AB＝ $\text{[math]}$ ，CD＝3，将Rt△CDE沿BA向左平移．
1. （1）当点C第一次落到⊙O上时，此时记为点 $\text{[math]}$ ．求证： $\text{[math]}$ 与⊙O相切；
2. （2）当点C第二次落到⊙O上时，此时记为点 $\text{[math]}$ ．求 $\text{[math]}$ 、 $\text{[math]}$ 、弧 $\text{[math]}$ 围成的图形的面积．
答案解析收藏纠错 + 选题
26. (2021九下·盐城期中) 小明为了能在4月份的体育加试中取得好成绩，每天进行掷实心球训练：当投掷实心球时会产生竖直向上的速度和水平向前的速度，研究表明：当这两个速度相等时，投掷距离最远．实心球在投掷的过程中的高度y与实心球出手后的时间t满足：y＝－5t²＋bt＋2，水平距离x＝at，a是出手后实心球水平向前的速度，b为出手后竖直向上的速度．
1. （1）当 $\text{[math]}$ 时，
  ①写出x与t的函数表达式为，y与t的函数表达式为；
  
  ②结合所给的平面直角坐标系，求出y与x的函数表达式及此时投掷距离．
2. （2）当a＝b时，点O为投掷点，实心球落在圆心角为45°的∠AOB区域内时成绩有效，以实心球的落地点与投掷点O的距离为学生的投掷距离，已知落地点P在∠AOB区域内且到边界的距离PM＝ $\text{[math]}$ m，PN＝6m，求出小明投掷的距离及实心球在此次投掷中的最高高度．
答案解析收藏纠错 + 选题
27. (2021九下·盐城期中) 八年级下册，我们曾经探究过“一元一次方程、一元一次不等式与一次函数”之间的关系，学会了运用一次函数的图象可以解一元一次方程与一元一次不等式．例如：一次函数y=3x+2与x轴交点的横坐标是方程3x+2=0的解；一次函数y=3x+2在x轴上方部分图像的自变量取值范围是不等式3x+2>0的解集．
1. （1） 【类比解决】
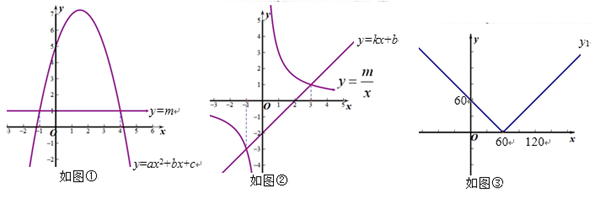
  利用图像解下列方程或不等式．
  
  Ⅰ.如图①，方程ax²＋bx＋c－m=0的解为；
  
  Ⅱ.如图②，不等式kx＋b< $\text{[math]}$ 的解为．
2. （2） 【拓展探究】
  已知函数y₁=|60－x|，y₂=|120－x|．
  
  Ⅰ.利用分类思想，可将函数y1=|60－x|先转化为 $\text{[math]}$ ，然后分别画出y1=60－x的图像x≤60的部分和y1=x－60的图像x＞60的部分，就可以得到函数y1=|60－x|的图像，如图③所示．请在图③所在的平面直角坐标系中直接画出y2=|120－x|的图像．
  
  Ⅱ.已知min{m，n} =m（m≤n），例如：min{1，－2} =－2．若y=min{y₁ ， y₂}的图像为W，请计算图像W与坐标轴围成图形的总面积．
3. （3） 【实际应用】
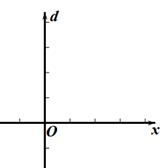
  有一条长为600米的步行道OA，A是垃圾投放点w1，若以O为原点，OA为x轴正半轴建立直角坐标系，设B（x，0），现要在步行道上建另一座垃圾投放点w2（t，0），点B与w1的距离为d1=|600－x|，点B与w2的距离为d2＝|x－t|，d表示与B点距离最近的垃圾投放点的距离，即：d＝min{d1，d2}．若可以通过函数d的图像与坐标轴围成的总面积来测算扔垃圾的便利程度，面积越小越便利．问：垃圾投放点w2建在何处才能比建在OA中点时更加便利?
答案解析收藏纠错 + 选题