湖北省随县2021年数学中考适应性试卷

更新时间：2021-06-26 浏览次数：160 类型：中考模拟

一、单选题

1. (2021七上·镇原期中) $\text{[math]}$ 的倒数是（）

A . 2021 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·新华月考) 下列调查中，适宜采用全面调查方式的是（）

A . 了解我县中小学生课后的手机使用情况 B . 了解一批手机电池的使用寿命 C . 了解我县初中生的视力情况 D . 了解全班学生参加社会实践活动的情况

答案解析收藏纠错 + 选题
3. (2021·随县模拟) 如图是一个正六棱柱的茶叶盒，其主视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·韩城模拟) 如图，直线AB∥CD，∠B＝50°，∠D＝20°，则∠E的度数是（）

A . 20° B . 30° C . 50° D . 70°

答案解析收藏纠错 + 选题
5. (2024七下·广水期末) 我国民间流传的数学名题：“只闻隔壁人分银，不知多少银和人，每人7两少7两，每人半斤多半斤，试问各位善算者，多少人分多少银？（1斤等于10两）”，其大意是：听见隔壁一些人在分银两，每人7两还缺7两，每人半斤则多半斤，问共有多少人？共有多少两银子？设有x个人，共分y两银子，根据题意，可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·随县模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的两不相等的实数根，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·随县模拟) 如图，PA、PB分别是⊙O的切线，A、B为切点，AC是⊙O的直径，已知∠BAC=35°，∠P的度数为（）

A . 35° B . 45° C . 65° D . 70°

答案解析收藏纠错 + 选题
8. (2021·随县模拟) 甲乙两地相距 $\text{[math]}$ ，小王从甲地匀速步行到乙地，同时，小张从乙地沿同一路线匀速步行前往甲地，两人之间的路程 $\text{[math]}$ 与小王步行的时间 $\text{[math]}$ 之间的函数关系如图中的折线段 $\text{[math]}$ 所示，已知小张先走完全程.结合图象，得到以下四个结论：

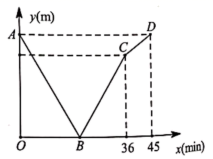
①小张的步行速度是 $\text{[math]}$ ；

②小王走完全程需要36分钟；

③图中B点的横坐标为22.5；

④图中点C的纵坐标为2880.

其中错误的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
9. (2021·随县模拟) 对点 $\text{[math]}$ 的一次操作变换记为 $\text{[math]}$ ，定义其变换法则如下： $\text{[math]}$ ；且规定 $\text{[math]}$ （n为大于1的整数）.如 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·随县模拟) 如图，抛物线 $\text{[math]}$ 的顶点坐标 $\text{[math]}$ ，与 $\text{[math]}$ 轴的一个交点 $\text{[math]}$ ，直线 $\text{[math]}$ 与抛物线交于 $\text{[math]}$ ， $\text{[math]}$ 两点，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③方程 $\text{[math]}$ 有两个不相等的实数根；④当 $\text{[math]}$ 时，则 $\text{[math]}$ .其中正确结论的个数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021·随县模拟) 代数式 $\text{[math]}$ 在实数范围内有意义，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
12. (2021·随县模拟) 人类进入 $\text{[math]}$ 时代，科技竞争日趋激烈.据报道，我国某种芯片的制作工艺已达到 $\text{[math]}$ 纳米并已实现量产，“中国芯”迎来技术新突破.已知 $\text{[math]}$ 纳米 $\text{[math]}$ 米，则 $\text{[math]}$ 纳米等于多少米？将其结果用科学记数法表示为.

答案解析收藏纠错 + 选题
13. (2021·随县模拟) 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ 的半径为4，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
14. (2021·随县模拟) 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是天．

答案解析收藏纠错 + 选题
15. (2021·随县模拟) 小君家购入如图1的划船机一台，如图2是划船机的部分示意图.阻尼轮 $\text{[math]}$ 由支架 $\text{[math]}$ 和 $\text{[math]}$ 支撑，点A处于点O的正下方， $\text{[math]}$ 与 $\text{[math]}$ 相切，脚踏板点E和圆心O在连杆 $\text{[math]}$ 上， $\text{[math]}$ 部分隐藏在阻尼轮内部，测量发现点E到地面的高度 $\text{[math]}$ 为35 $\text{[math]}$ ，E、A两点间的水平距离 $\text{[math]}$ 为72 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2021·随县模拟) 如图，矩形ABCD中，AB=6，AD=8，点P是AB边上一动点，把△ADP沿DP折叠得△ $\text{[math]}$ ，射线 $\text{[math]}$ 交直线AB于点Q点.
1. （1）当Q点和B点重合时，PQ长为；
2. （2）当△ $\text{[math]}$ 为等腰三角形时，DQ长为.
答案解析收藏纠错 + 选题

三、解答题

17. (2021·随县模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2021·随县模拟) 在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于 $\text{[math]}$ .求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题

19. (2021·随县模拟) 某校在第五届全国学生“学宪法讲宪法”活动中举办了宪法知识竞赛，并从中选取了部分学生的竞赛成绩进行统计（满分100分，成绩均不低于50分），绘制了如下尚不完整的统计图表.

调查结果频数分布表

分数段/分	频数	频率
50≤x＜60	2	0.04
60≤x＜70	8	0.16
70≤x＜80	m	0.24
80≤x＜90	24	n
90≤x＜100	4	0.08

请根据以上信息，回答下列问题：

（1）填空：m＝，n＝，本次抽取了名学生；
（2）请补全频数分布直方图；
（3）若甲同学的竞赛成绩是所有竞赛成绩的中位数，据此推测他的成绩落在分数段内；
（4）竞赛成绩不低于90分的4名同学中正好有2名男生和2名女生，现准备从中随机选出2名同学参加市里面“学宪法讲宪法”演讲比赛，求正好抽到一男一女的概率.

答案解析收藏纠错 + 选题

20. (2021·随县模拟) 如图，反比例函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ 和点 $\text{[math]}$ .
1. （1）求反比例函数的解析式和点 $\text{[math]}$ 的坐标；
2. （2）连接 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
3. （3）结合图象，请直接写出使反比例函数值小于一次函数值的自变量 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
21. (2021·随县模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 分别与 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并证明你的结论；
2. （2）若 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ ，求阴影部分的面积.
答案解析收藏纠错 + 选题

22. (2021·随县模拟) 2020年受疫情影响，大规模的聚会活动需要采取很多防控措施，比如各种社会性考试增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况，调查了某场考试上午考生进入考点的累计人数 $\text{[math]}$ （人）与时间 $\text{[math]}$ （分钟）的变化情况，数据如下表：（表中 $\text{[math]}$ 表示 $\text{[math]}$ ）

时间 $\text{[math]}$ （分钟）	0	1	2	3	4	5	6	7	8	9	$\text{[math]}$
人数 $\text{[math]}$ （人）	0	170	320	450	560	650	720	770	800	810	810

（1）请在给定的坐标系内按上列表格数据将这15分钟内考生进入考点的累计人数与时间关系进行描点，并将这些点用平滑的线条连接起来；
（2）根据你所画图形的变化规律，利用初中所学函数知识求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
（3）如果考生一进考点就开始测量体温，体温检测点有2个，每个检测点每分钟检测20人，考生排队测量体温，求排队人数最多时有多少人？

答案解析收藏纠错 + 选题

23. (2022八上·镇海区期中) 从三角形（不是等腰三角形）一个顶点引出的一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形有两角对应相等，我们把这条线段叫做这个三角形的“优美分割线”.
1. （1）如图，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°，求证：CD为△ABC的“优美分割线”.
2. （2）在△ABC中，∠A＝46°，CD为△ABC的“优美分割线”且△ACD为等腰三角形，求∠ACB的度数.
3. （3）在△ABC中，∠A＝30°，AC＝6，CD为△ABC的“优美分割线”，且△ACD是等腰三角形，求线段BD的长.
答案解析收藏纠错 + 选题
24. (2021·随县模拟) 已知二次函数y＝ax²＋bx＋6的图像开口向下，与x轴交于点A（－6，0）和点B（2，0），与y轴交于点C，点P是该函数图象上的一个动点（不与点C重合）
1. （1）求二次函数的关系式；
2. （2）如图1当点P是该函数图象上一个动点且在线段 $\text{[math]}$ 的上方，若△PCA的面积为12，求点P的坐标；
3. （3）如图2，该函数图象的顶点为D，在该函数图象上是否存在点E，使得∠EAB＝2∠DAC，若存在请直接写出点E的坐标；若不存在请说明理由.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

湖北省随县2021年数学中考适应性试卷

副标题：

*注意事项：

湖北省随县2021年数学中考适应性试卷

试题分析

总体分析

题量分析

难度分析

知识点分析