浙江省湖州市2020-2021学年八年级下学期数学期中考试试...

更新时间：2024-07-13 浏览次数：229 类型：期中考试

一、选择题（本题有10小题，每小题3分，共30分）

1. (2023·庐江模拟) 下列常用手机 APP 的图标中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021八下·湖州期中) 若代数式 $\text{[math]}$ 在实数范围内有意义，则 $\text{[math]}$ 的取值范围是（）

A . x≥-2 B . x＞-2 C . $\text{[math]}$ D . x＞2

答案解析收藏纠错 + 选题
3. (2021八下·湖州期中) 用配方法解方程 $\text{[math]}$ ，变形结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021八下·湖州期中) 下列等式：① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ ，④ $\text{[math]}$ ⑤ $\text{[math]}$ ，⑥ $\text{[math]}$ ；正确的有（）个

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题
5. (2021八下·湖州期中) 有一组数据：2，5，5，6，7，这组数据的方差为（）

A . 2.6 B . 2.8 C . 3 D . 3.2

答案解析收藏纠错 + 选题
6. (2021八下·湖州期中) 已知a是整数，且 $\text{[math]}$ ＜a＜ $\text{[math]}$ ，则整数a有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. (2021八下·湖州期中) 用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”，应先假设（）

A . 两个锐角都小于45° B . 两个锐角都大于45° C . 有一个锐角小于45° D . 有一个锐角大于或等于45°

答案解析收藏纠错 + 选题
8. (2021八下·湖州期中) 某种商品原价是100元，经两次降价后的价格是90元.设平均每次降价的百分率为 $\text{[math]}$ ，可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021八下·湖州期中) 关于x的一元二次方程（a≠0），下列命题：①若a、c异号，则方程必有两个不相等的实数根；②若，则方程有一个根为-2；③若方程的两根互为相反数，则； ④若，则方程有两个不相等的实数根.其中真命题为（）

A . ①②④ B . ①②③ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题
10. (2021八下·湖州期中) 如图，平行四边形ABCD中，AB=6，BC=4，∠DAB=60°，E在AB上，且AE= $\text{[math]}$ EB，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则DP：DQ的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2021八下·湖州期中) 已知一个正多边形的每个外角等于60°，则这个正多边形是边形.

答案解析收藏纠错 + 选题
12. (2021八下·湖州期中)
某射击俱乐部将 $\text{[math]}$ 名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图．由图可知， $\text{[math]}$ 名成员射击成绩的中位数是环．

答案解析收藏纠错 + 选题
13. (2022八下·温州期中) 若关于x的方程 $\text{[math]}$ 有两个不相等的实数根，则k的取值范围是.

答案解析收藏纠错 + 选题
14. (2021八下·湖州期中) 如图，点A，B为定点，定直线 $\text{[math]}$ ∥AB，P是 $\text{[math]}$ 上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小.其中会随点P的移动而变化的是.

答案解析收藏纠错 + 选题
15. (2021八下·湖州期中) 如图，在平行四边形ABCD中，AB=6，AD=8，∠B=60°，∠BAD 与∠CDA的角平分线AE、BF相交于点G，且交BC于点E、F，则图中阴影部分的面积是.

答案解析收藏纠错 + 选题
16. (2021八下·湖州期中) 如图，在平面直角坐标系xOy中，平行四边形OABC的顶点A、B的坐标分别为（12，0）、（14，6），将□OABC绕点O逆时针方向旋转得到平行四边形O $\text{[math]}$ ，当点 $\text{[math]}$ 落在BC的延长线上时，线段 $\text{[math]}$ 交BC于点E，则线段 $\text{[math]}$ 的长度为.

答案解析收藏纠错 + 选题

三、解答题（本大题共7小题，共66）

17. (2021八下·湖州期中) 计算题
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2021八下·湖州期中) 解下列方程
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2021八下·湖州期中) 已知：如图，在四边形ABCD中，AB//CD，E、F为对角线AC上两点，且AE=CF，DF//BE.求证：四边形ABCD是平行四边形.

答案解析收藏纠错 + 选题
20. (2021八下·湖州期中) 如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．

答案解析收藏纠错 + 选题

21. (2021八下·湖州期中) 某校德育处积极开展“预防新冠病毒知识知多少”宣传活动，组织举办了一次防病毒知识竞赛，本次竞赛满分10分，学生得分均为整数，成绩达到6分及6分以上为合格，达到9分或10分为优秀.在这次竞赛中，甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.

组别	平均分	中位数	方差	合格率	优秀率
甲组	6.8	a	3.76	90%	30%
乙组	b	7.5	1.96	80%	20%

解答下列问题：

（1）填空：a＝；b＝.
（2）小敏说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上.”观察上面表格后思考判断，小敏属于（填“甲”或“乙”）组的学生.
（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩比乙组好.但乙组同学不同意甲组同学的说法，认为他们的成绩要好于甲组请你写出两条支持乙组同学观点的理由.

答案解析收藏纠错 + 选题

22. (2021八下·湖州期中) 有一种螃蟹，从海上捕获后不放养最多只能存活两天，如果放养在塘内，可以延长存活时间，但每天也会有一定数量的螃蟹死去，假设放养期间内螃蟹的个体重量基本保持不变.现有一经销商，按市场价收购了这种活螃蟹1000kg放养在塘内，此时市场价为30元/kg.据测算此后每千克的活蟹的市场价每天可上升1元，但是，放养一天各种费用支出400元，且平均每天还有10 kg的蟹死去，假定死蟹均于当天全部售出，售价都是20元/kg .
1. （1）设x天后每千克活蟹的市场价为p元，请写出p关于x的函数关系式；
2. （2）如果经销商将这批蟹出售后能获利6250元，那么他应放养多少天后再一次性售出?
答案解析收藏纠错 + 选题
23. (2021八下·湖州期中) 如图，在△ABC中，∠ACB=90°，以点B为圆心，BC长为半径画弧，交线段AB于点D；以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD．
1. （1）若∠A=28°，求∠ACD的度数．
2. （2）设BC=a，AC=b．
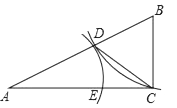
  ①线段AD的长是方程x²+2ax﹣b²=0的一个根吗？说明理由．
  ②若AD=EC，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2021八下·湖州期中) 我们规定：有一组邻边相等，且这组邻边的夹角为60°的凸四边形叫做“准筝形”.
1. （1）如图1，在四边形ABCD中，∠A+∠C＝270°，∠D＝30°，AB＝BC，求证：四边形ABCD是“准筝形”；
2. （2）小军同学研究 “准筝形”时，思索这样一道题：如图2，“准筝形”ABCD，AD＝BD，∠BAD＝∠BCD＝60°，BC＝5，CD＝3，求AC的长.
  小军研究后发现，可以CD为边向外作等边三角形，构造手拉手全等模型，用转化的思想来求AC.请你按照小军的思路求AC的长.
3. （3）如图3，在△ABC中，∠A＝45°，∠ABC＝120°，BC＝2 $\text{[math]}$ ，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时，请直接写出四边形ABCD的面积.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省湖州市2020-2021学年八年级下学期数学期中考试试...

副标题：

*注意事项：

浙江省湖州市2020-2021学年八年级下学期数学期中考试试...

试题分析

总体分析

题量分析

难度分析

知识点分析