 B .
B .  C .
C .  D .
D . 

(参考数据: ,
,
,
,
)


|
|
… |
-6 |
-4 |
-2 |
-1 |
-0.5 |
0.5 |
1 |
|
4 |
6 |
… |
|
|
… |
|
|
-4 |
-5 |
|
|
5 |
4 |
5 |
|
… |

初中一体机管理员的测试成绩在 组中的数据为:81,85,88.
新高中一体机管理员的测试成绩:76,83,71,100,81,100,82,88,95,90,100,86,89,93,86.
成绩统计表如表:(注:极差为样本中最大数据与最小数据的差)
| 校部 | 平均数 | 中位数 | 最高分 | 众数 | 极差 |
| 初中 | 88 | | 98 | 98 | 32 |
| 新高中 | 88 | 86 | 100 | | |
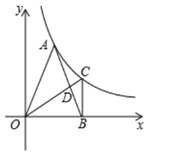
①当点 、
、
三点共线时,求证:
;
②若 交
于点
,且
,
,请直接写出
的值.