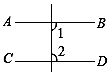
 B .
B . 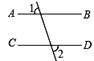 C .
C . 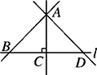
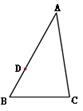
①过点A有且只有一条直线AC垂直于直线l;
②线段AC的长是点A到直线l的距离;
③线段AB,AC,AD中,线段AC最短,根据是两点之间线段最短;
④线段AB,AC,AD中,线段AC最短,根据是垂线段最短.
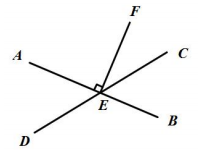

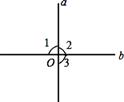
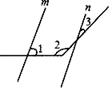

小禹看到小华的改错后说:“你还有错没有改出来.”
小华还有哪些错误没有改出来?请你帮助小华把第一步中的其他错误圈画出来,再完成此题的正确解答过程.
如图,AB∥CD,∠C=∠D,如果∠1=∠2,那么∠E与∠C
互为补角吗?说说你的理由.
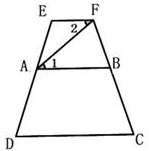
解:因为∠1=∠2,
根据 ▲ ,
所以EF∥ ▲ .
又因为AB∥CD,
根据 ▲ ,
所以EF∥ ▲ .
根据 ▲ ,
所以∠E+ ▲ = ▲ °.
又因为∠C=∠D,
所以∠E+ ▲ = ▲ °,
所以∠E与∠C互为补角.
|
x(人) |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
… |
|
y(元) |
﹣3000 |
﹣2000 |
﹣1000 |
0 |
1000 |
2000 |
… |
我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.
小明同学用如图1所示不同颜色的正方形与长方形纸片拼成了一个如图2所示的正方形.
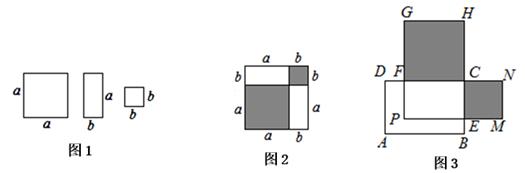
如果x满足(6-x)(x-2)=3.求(6-x)2+(x-2)2 的值。
小明想:如果设6-x=m,x-2=n ,那要求的式子就可以写成m2+n2了
请你按照小明的思路完成这道题目。
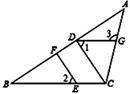
如图2,射线OM与射线ON交于点O,直线m∥n,直线m分别交OM、ON于点A、D,直线n分别交OM、ON于点B、C,点P在射线OM上运动.
①当点P在A、B(不与A、B重合)两点之间运动时,设∠ADP=∠α,∠BCP=∠β.则∠CPD,∠α,∠β之间有何数量关系?请说明理由;
②若点P不在线段AB上运动时(点P与点A、B、O三点都不重合),请你画出满足条件的所有图形并直接写出∠CPD,∠α,∠β之间的数量关系.