北京市平谷区2021年中考数学二模试卷

更新时间：2024-07-13 浏览次数：161 类型：中考模拟

一、单选题

1. (2021·平谷模拟) 2022年冬奥会张家口主场馆的设计方案日前正式对外公布，场馆主题为“活力冰雪，激情四射”，占地面积50公顷，规划总建筑面积为270000平方米．将270000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·盐田模拟) 如图是某几何体的三视图，则该几何体是（）

A . 圆锥 B . 圆柱 C . 三棱柱 D . 三棱锥

答案解析收藏纠错 + 选题
3. (2021·平谷模拟) 有理数 $\text{[math]}$ ， $\text{[math]}$ 在数轴上的对应点的位置如图所示，则结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·平谷模拟) 中国花卉博览会（简称“花博会”）是中国规模最大、档次最高、影响最广的国家级花事盛会，被称为中国花卉界的“奥林匹克”．下列花博会会徽图案中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024八上·昭通月考) 一个多边形的内角和是720°，这个多边形是（）

A . 五边形 B . 六边形 C . 七边形 D . 八边形

答案解析收藏纠错 + 选题
6. (2021·平谷模拟) 若 $\text{[math]}$ ＝2， $\text{[math]}$ ＝3，则 $\text{[math]}$ 的值为（）

A . 6 B . 5 C . 3 D . 2

答案解析收藏纠错 + 选题
7. (2021·平谷模拟) 如图，△ABC中，AB＝AC ， AD⊥BC于D ， BE⊥AC于E ，则以下两个角的关系中不成立的是（）

A . ∠1＝∠2 B . ∠3＝∠2 C . ∠4＝∠5 D . ∠4＝∠C

答案解析收藏纠错 + 选题
8. (2021·平谷模拟) 目标达成度也叫完成率，一般是指个体的实际完成量与目标完成量的比值，树立明确具体的目标，能够帮助人们更好的自我认知，迅速成长．某销售部门有9位员工（编号分别为A－I），下图是根据他们月初制定的目标销售任务和月末实际完成情况绘制的统计图，下列结论正确的是（）

①E超额完成了目标任务；②目标与实际完成相差最多的是G；

③H的目标达成度为100%；④月度达成率超过75%且实际销售额大于4万元的有三个人．

A . ①②③④ B . ①③ C . ① ②③ D . ②③④

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·桦甸期末) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是.

答案解析收藏纠错 + 选题
10. (2021·宾阳模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2021·平谷模拟) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2021·平谷模拟) 如图所示的网格是正方形网格， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是网格线交点， $\text{[math]}$ 恰好经过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，OD为与网格线重合的一条半径，则∠ABC 与∠AOD大小关系为：∠ABC ∠AOD（填“＞”，“＝”或“＜”）．

答案解析收藏纠错 + 选题
13. (2024八上·昌平期中) 化简： $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题

14. (2021·平谷模拟) 某农场引进一批新菜种，在播种前做了五次发芽实验，每次任取一定数量的种子进行实验．实验结果如下表所示：

实验的菜种数	200	500	1000	2000	10000
发芽的菜种数	193	487	983	1942	9734
发芽率	0.965	0.974	0.983	0.971	0.973

在与实验条件相同的情况下，估计种一粒这样的菜种发芽的概率为．（精确到 0.01 ）

答案解析收藏纠错 + 选题

15. (2021·平谷模拟) 如图，线段CE的长为3cm ，延长EC到B ，以CB为一边作正方形ABCD ，连接DE ，以DE为一边作正方形DEFG ，设正方形ABCD的面积为 $\text{[math]}$ ，正方形DEFG的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

16. (2021·平谷模拟) 母亲节来临之际，小凡同学打算用自己平时节省出来的50元钱给母亲买束鲜花，已知花店里鲜花价格如表：

百合	薰衣草	玫瑰	蔷薇	向日葵	康乃馨
12元/支	2元/支	5元/支	4元/支	15元/支	3元/支
母亲节期间包装免费

小凡想用妈妈喜欢的百合、玫瑰、康乃馨这三种花组成一个花束，若三种花都要购买且50元全部花净，请给出一种你喜欢的组成方式，百合、玫瑰、康乃馨的支数分别为．

答案解析收藏纠错 + 选题

三、解答题

17. (2021·平谷模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021·平谷模拟) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2021·平谷模拟) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
20. (2021·平谷模拟) 已知关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根．
1. （1）求k的取值范围；
2. （2）若k为满足条件的最大的整数，求此时方程的解．
答案解析收藏纠错 + 选题
21. (2021·平谷模拟) 已知：如图，锐角△ABC ．

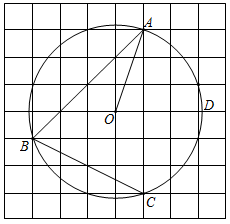
求作：在AB上取点D ， AC上取点E ，使得 $\text{[math]}$ ，作法：

①分别以点B和点C为圆心，大于 $\text{[math]}$ 长为半径画弧，两弧相交于点M、N ，作直线MN ，交BC于点O；

②以点O为圆心，OB长为半径画圆，在BC上方交AB于点D ，交AC于点E；

③连接 $\text{[math]}$ ， $\text{[math]}$ 即为所求作
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
2. （2）完成下面的证明
  证明：∵点B、C、E、D均在 $\text{[math]}$ 上．
  
  ∴ $\text{[math]}$ （）（填推理依据）．
  
  ∵ $\text{[math]}$
  
  ∴ $\text{[math]}$ ▲ ．
  
  ∵ $\text{[math]}$
  
  ∴ $\text{[math]}$
答案解析收藏纠错 + 选题
22. (2021·平谷模拟) 如图，在平面直角坐标系xOy中，直线 $\text{[math]}$ 经过点A(0，－1)和点B(3，2)．
1. （1）求直线 $\text{[math]}$ 的表达式；
2. （2）已知双曲线 $\text{[math]}$ ．
  ①当双曲线 $\text{[math]}$ 经过点B时，求m的值；
  
  ②若当 $\text{[math]}$ 时，总有 $\text{[math]}$ 直接写出m的取值范围．
答案解析收藏纠错 + 选题
23. (2021八下·铁锋期末) 如图，在Rt△ABC中，∠ACB＝90°，D ， E分别是边AB ， BC的中点，连接DE并延长到点F ，使EF＝DE ，连接CF ， BF ．
1. （1）求证：四边形CFBD是菱形；
2. （2）连接AE ，若CF＝ $\text{[math]}$ ，DF＝2，求AE的长．
答案解析收藏纠错 + 选题
24. (2021·平谷模拟) 如图，AB是 $\text{[math]}$ 直径，点C是 $\text{[math]}$ 上一点，过点C作 $\text{[math]}$ 的切线CG ，过点B作CG的垂线，垂足为点D ，交 $\text{[math]}$ 于点E ，连接CB ．
1. （1）求证：CB平分∠ABD；
2. （2）若 $\text{[math]}$ ，BC＝5，求CE长．
答案解析收藏纠错 + 选题
25. (2021·平谷模拟) “传递爱心，传播文明”某校学生积极参加首都志愿者服务，为了了解某校九年级学生参加志愿者服务的情况，明明和飞飞一起随机调查了该校九年级50名学生的志愿者服务时长数据，并用两种不同方法分别对数据进行了整理、描述，下面给出了部分信息：
a ．明明对50名学生的志愿者服务时长数据进行分组整理，绘制了如下频数分布直方图（数据分成5组：0≤x＜10，10≤x＜20，20≤x＜30， 30≤x＜40，40≤x）：

B.其中志愿者服务时长在20≤x＜30这一组的数据是：20；20；21；22；23；23；23；23；25；26；26；26；27；28；28；29

c ．飞飞通过调查发现，这50名学生的志愿者服务类型主要集中在：敬老院服务、扶贫助残、环境卫生、文化宣传等几个方面，他从50名学生的志愿者服务时长不同类型角度对数据进行整理，绘制了如下扇形统计图；

请根据所给信息，解答下列问题：
1. （1）请补全频数分布直方图；
2. （2）这50名学生服务时长的中位数是；
3. （3）扇形统计图中n的值为；
4. （4）据了解随机抽取的50名学生的志愿者时长中恰好有300个小时是参加文化宣传的，则他们参加志愿者服务时长的平均值为；
5. （5）若该校九年级共有学生500人，请估计该校九年级学生中参加志愿者服务时长不低于30个小时的约有人．
答案解析收藏纠错 + 选题
26. (2021·平谷模拟) 已知抛物线 $\text{[math]}$ ，
1. （1）直接写出该抛物线的对称轴及顶点坐标；
2. （2）已知该抛物线经过 $\text{[math]}$ 两点，
  ①直接写出 $\text{[math]}$ 的大小关系；
  
  ②过B点垂直于x轴的直线交x轴于点C ，若四边形AOCB的面积小于或等于6，直接写出a的取值范围．
答案解析收藏纠错 + 选题
27. (2021·平谷模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ，G是AB边上一点，过点G作射线CP ，过点A作 $\text{[math]}$ 于点M ，过点B作 $\text{[math]}$ 于点N ．
1. （1）求证：CM＝BN；
2. （2）取AB中点O ，连接OM、ON ，依题意补全图形，猜想线段BN、AM、OM的数量关系，并证明；
答案解析收藏纠错 + 选题
28. (2021·平谷模拟) 对于平面直角坐标系 $\text{[math]}$ 中的一点 $\text{[math]}$ 和 $\text{[math]}$ ，给出如下的定义：若 $\text{[math]}$ 上存在一个点 $\text{[math]}$ ，连接PA ，将射线PA绕点P顺时针旋转90°得到射线PM ，若射线PM与 $\text{[math]}$ 相交于点B ，则称 $\text{[math]}$ 为 $\text{[math]}$ 的直角点．
1. （1）当 $\text{[math]}$ 的半径为 $\text{[math]}$ 时，
  ①在点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 中， $\text{[math]}$ 的直角点是 ▲ ．
  
  ②已知直线 $\text{[math]}$ ： $\text{[math]}$ ，若直线 $\text{[math]}$ 上存在 $\text{[math]}$ 的直角点，求 $\text{[math]}$ 的取值范围．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 的半径为 $\text{[math]}$ ，直线 $\text{[math]}$ 上存在 $\text{[math]}$ 的直角点，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题