
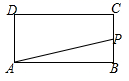
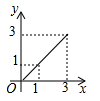 B .
B . 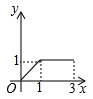 C .
C . 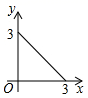 D .
D . 
①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;③面积相等的两个三角形是全等图形;④全等三角形的周长相等其中正确的结论个数是( )

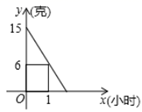

其中(2x+1)2+|y﹣2|=0.
|
所挂物体质量x/kg |
0 |
1 |
2 |
3 |
4 |
5 |
|
弹簧长度y/cm |
18 |
20 |
22 |
24 |
26 |
28 |
解:设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面问题:


