广东省深圳市光明区2020-2021学年七年级下学期数学期末...

更新时间：2021-10-11 浏览次数：302 类型：期末考试

一、单选题

1. (2021七下·光明期末) 下列汉字中，不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021七下·光明期末) 某条信息一周内被转发0.0000218亿次，将数据0.0000218科学记数法表示为（）

A . 2.18×10^﹣6 B . 2.18×10⁶ C . 2.18×10^﹣5 D . 2.18×10⁵

答案解析收藏纠错 + 选题
3. (2021七下·光明期末) 下列计算一定正确的是（）

A . （﹣a³）²＝a⁵ B . a³÷a³＝0 C . （﹣a）³+a³＝1 D . a²﹣2a²＝﹣a²

答案解析收藏纠错 + 选题
4. (2021七下·光明期末) 下列事件中，是必然事件的是（）

A . 明天北京新冠肺炎新增0人 B . 车辆随机到达一个路口，遇到红灯 C . 如果a²＝b² ，那么a＝b D . 将花生油滴在水中，油会浮在水面上

答案解析收藏纠错 + 选题
5. (2022·肇源模拟) 如图是一个4×4的方格，若在这个方格内投掷飞镖，则飞镖恰好落在阴影部分的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021七下·光明期末) 如图，已知点A、D、C、F在同一直线上，AB＝DE，添加下列条件后，仍不能判断△ABC≌△DEF的是（）

A . BC＝EF B . ∠A＝∠EDF C . AB $\text{[math]}$ DE D . ∠BCA＝∠EDF

答案解析收藏纠错 + 选题
7. (2021七下·盐湖期中) 如图，点P在直线l外，点A、B在直线l上，PA=4，PB＝7，则点P到直线l的距离可能是（）

A . 3 B . 4 C . 5 D . 7

答案解析收藏纠错 + 选题
8. (2021七下·当涂期末) 如图，在下列条件中，能判断AB∥CD的是（）

A . ∠1＝∠2 B . ∠BAD＝∠BCD C . ∠BAD＋∠ADC＝180° D . ∠3＝∠4

答案解析收藏纠错 + 选题
9. (2021七下·光明期末) 如图，a∥b，∠ABD的平分线交直线a于点C，CE⊥直线c于点E，∠1＝24°，则∠2的大小为（）

A . 114° B . 142° C . 147° D . 156°

答案解析收藏纠错 + 选题
10. (2021七下·光明期末) 如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P， $\text{[math]}$ ，PG $\text{[math]}$ AD交BC于F，交AB于G，① $\text{[math]}$ ；②S_△PAC：S_△PAB＝PC：PB；③BP垂直平分CE；④∠PCF＝∠CPF．其中正确的有（）

A . ①②④ B . ①③④ C . ②③④ D . ①③

答案解析收藏纠错 + 选题

二、填空题

11. (2021七下·光明期末) （﹣2）^﹣1＝．

答案解析收藏纠错 + 选题
12. (2024七下·罗湖期末) 定义：如果一个数的平方等于﹣1，记为i²＝﹣1，这个数i叫做虚数单位，那么：（1+2i）（1﹣2i）＝．

答案解析收藏纠错 + 选题
13. (2021七下·光明期末) 如图，在△ABC中，∠B＝65°，∠C＝28°，分别以点A和点C为圆心，大于 $\text{[math]}$ 画弧，两弧相交于点M，N，作直线MN，连接AD，则∠BAD的度数为．

答案解析收藏纠错 + 选题
14. (2023七下·坪山月考) 如图，在△ABC中，AD是BC边上的高，BE是AC边上的高，且AD、BE的交于点F，若BF＝AC，CD=6，BD＝8，则线段AF的长度为．

答案解析收藏纠错 + 选题
15. (2021七下·光明期末) 如图，在△ABC中，E是AC的中点，AD，CF，BE交于一点G，BC＝3DC，S_△GEC＝3，S_△GBD＝8，则△ABC的面积是．

答案解析收藏纠错 + 选题

三、解答题

16. (2021七下·光明期末) 计算：
1. （1） |﹣2|+（﹣2）²+（3.14﹣π）⁰﹣（ $\text{[math]}$ ）^﹣1 ．
2. （2）（﹣2x）³÷x﹣（﹣x）² ．
答案解析收藏纠错 + 选题
17. (2021七下·光明期末) 先化简，再求值：[（x﹣2y）（x+2y）﹣x（x﹣2y）]÷（2y），其中x＝1，y＝﹣2．

答案解析收藏纠错 + 选题
18. (2021七下·光明期末) 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
1. （1）在图中画出与△ABC关于直线l成轴对称的A₁B₁C₁；
2. （2） △A₁B₁C₁的面积是；
3. （3）利用网格线在直线上求作一点P，使得PA+PC最小，请在直线l上标出点P位置．
答案解析收藏纠错 + 选题
19. (2022七下·历城期末) 在一个口袋中只装有4个白球和6个红球，它们除颜色外完全相同.
1. （1）事件“从口袋中随机摸出一个球是绿球”发生的概率是；
2. （2）事件“从口袋中随机摸出一个球是红球”发生的概率是；
3. （3）现从口袋中取走若干个红球，并放入相同数量的白球，充分摇匀后，要使从口袋中随机摸出一个球是白球的概率是 $\text{[math]}$ ，求取走了多少个红球？
答案解析收藏纠错 + 选题
20. (2021七下·光明期末) 小明骑单车上学，当他骑了一段路时，想起要买某本书，买到书后继续去学校．以下是他本次上学所用的时间与离家距离的关系示意图．
根据图中提供的信息回答下列问题：
1. （1）小明家到学校的路程是米．
2. （2）本次上学途中，小明一共行驶了米．一共用了分钟．
3. （3）在整个上学的途中最快的速度是米/分．
4. （4）小明当出发分钟离家1200米．
答案解析收藏纠错 + 选题
21. (2021七下·光明期末) 填空：（将下面的推理过程及依据补充完整）
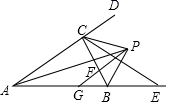
已知：△ABC的高AD所在直线与高BE所在直线相交于点F，过点F作FG $\text{[math]}$ BC，交直线AB于点G．如图，且∠ABC＝45°．

求证：①△BDF≌△ADC；②FG+DC＝AD；

①证明：∵AD，BE为高

∴∠ADB＝∠BEC＝90°

∵∠ABC＝45°

∴∠BAD＝∠   ▲   ＝45°

∴AD＝   ▲   ；

∵∠BEC＝90°

∴∠CBE+∠C＝90°（    ）

又∵∠DAC+∠C＝90°

∴∠CBE＝∠DAC（    ）

在△FDB和△CDA中，

∵∠FDB＝∠CDA＝90°，

AD＝BD

∠CBE＝∠DAC

∴△FDB≌△CDA（    ）

②∵△FDB≌△CDA，

∴DF＝DC（    ）

∵GF $\text{[math]}$ BC

∴∠AGF＝∠ABC＝45°，（    ）

∴∠AGF＝∠   ▲   ，

∴FA＝FG；

∴FG+DC＝FA+DF＝AD．

答案解析收藏纠错 + 选题
22. (2021七下·光明期末) 如图，AD $\text{[math]}$ BC，∠BAD的平分线交BC于点G．∠BCD＝90°．
1. （1）试说明：∠BAG＝∠BGA：
2. （2）如图2，∠BCD的平分线交AD于点E交射线GA于点F，
  ①写出∠AFC，∠BAG的数量关系，并说明理由．
  
  ②若∠ABG＝55°，则∠AFC＝ ▲ ．
3. （3）如图3，线段AG上有点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，则 $\text{[math]}$ 的值是．
答案解析收藏纠错 + 选题