浙江省嘉兴市2020-2021学年七年级下学期数学期末考试试...

更新时间：2024-07-13 浏览次数：272 类型：期末考试

一、选择题(每小题3分,共30分)

1. (2021七下·嘉兴期末) 计算x•x² ，结果正确的是（）

A . x² B . x³ C . x⁴ D . x⁵

答案解析收藏纠错 + 选题
2. (2023七下·瑞安期中) 如图，直线a ， b被直线c所截，∠1的同旁内角是（）

A . ∠2 B . ∠3 C . ∠4 D . ∠5

答案解析收藏纠错 + 选题
3. (2021七下·嘉兴期末) 观察下列五幅图案，在②③④⑤中可以通过①平移得到的是（）

A . ② B . ③ C . ④ D . ⑤

答案解析收藏纠错 + 选题
4. (2021七下·嘉兴期末) 已知 $\text{[math]}$ 是方程mx﹣y＝3的解，则m的值是（）

A . ﹣1 B . 1 C . ﹣7 D . 7

答案解析收藏纠错 + 选题
5. (2022七下·诸暨月考) 下列由左边到右边的变形中，属于因式分解的是（）

A . （a+1）（a﹣1）＝a²﹣1 B . a²﹣6a+9＝（a﹣3）² C . a²+2a+1＝a（a+2）+1 D . a²﹣5a＝a²（1﹣ $\text{[math]}$ ）

答案解析收藏纠错 + 选题
6. (2021七下·嘉兴期末) 小周将2020年某商场篮球销售情况的有关数据统计如图，若A品牌年销售量3000个，则B品牌年销售量（）

A . 3360个 B . 4000个 C . 4200个 D . 4500个

答案解析收藏纠错 + 选题
7. (2021七下·嘉兴期末) 用加减消元法解二元一次方程组 $\text{[math]}$ 时，下列方法中能消元的是（）

A . ①×2+② B . ①×2﹣② C . ①×3+② D . ①×（﹣3）﹣②

答案解析收藏纠错 + 选题
8. (2021七下·嘉兴期末) 化简（a﹣ $\text{[math]}$ ）÷ $\text{[math]}$ 结果正确的是（）

A . $\text{[math]}$ B . a﹣b C . $\text{[math]}$ D . a+b

答案解析收藏纠错 + 选题
9. (2024八下·织金月考) 若x²﹣bx﹣10＝（x+5）（x﹣a），则a^b的值是（）

A . ﹣8 B . 8 C . ﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七上·湖北期中) 曹老师有一包糖果，若分给m个学生，则每个学生分a颗，还剩b颗（b＜a）；若分给（m+10）个学生，则每个学生分3颗，还剩（b+1）颗，则a的值可能是（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题

二、填空题(本题有10小题,每小题3分,共30分)

11. (2024七下·杭州期中) 计算：2x•（﹣3xy）＝．

答案解析收藏纠错 + 选题
12. (2022七下·鄞州期末) 已知某组数据的频数为63，样本容量为90，则频率为．

答案解析收藏纠错 + 选题
13. (2021七下·嘉兴期末) 若分式 $\text{[math]}$ 有意义，则x的取值应该满足．

答案解析收藏纠错 + 选题
14. (2021七下·嘉兴期末) 因式分解：a³﹣a=．

答案解析收藏纠错 + 选题
15. (2021七下·嘉兴期末) 某种病毒的直径是0.00000007米，这个数据用科学记数法表示为米．

答案解析收藏纠错 + 选题
16. (2021七下·嘉兴期末) 如图，将一张长方形纸条ABCD沿EF折叠，若∠EFG＝47°，则∠BGP＝．

答案解析收藏纠错 + 选题
17. (2021七下·嘉兴期末) 已知a﹣b＝7，ab＝2，则（a+b）²＝．

答案解析收藏纠错 + 选题
18. (2021七下·嘉兴期末) 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我们古代货币单位）；马三匹、牛五头，共价三十八两．问马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为．

答案解析收藏纠错 + 选题
19. (2021七下·嘉兴期末) 若9^a·27^b÷81^c＝9，则2c﹣a﹣ $\text{[math]}$ b的值为．

答案解析收藏纠错 + 选题
20. (2021七下·嘉兴期末) 某几何体是由棱长为1厘米的正方体放置在桌面上搭建而成，每一层从上到下按如图所示的规律排列，一共n层．若将几何体的露出部分都涂上油漆（不含底面），则涂油漆面的面积为平方厘米（用n的代数式表示）．

答案解析收藏纠错 + 选题

三、解答题(第21~24题,每题6分,第25、26题,每题8分,共40分)

21. (2021七下·嘉兴期末)
1. （1）计算：（14x³﹣7x²）÷（7x）；
2. （2）解方程组： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2024七下·瑞金期中) 如图，已知∠DEB＝100°，∠BAC＝80°．
1. （1）判断DF与AC的位置关系，并说明理由；
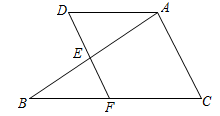
2. （2）若∠ADF＝∠C ， ∠DAC＝120°，求∠B的度数．
答案解析收藏纠错 + 选题

23. (2021七下·嘉兴期末) 为了解某市初中开展“垃圾分类”知识竞赛成绩情况，现从中随机抽取部分学生进行调查，并将调查结果绘制如下统计图表：

某市部分学生“垃圾分类”知识竞赛成绩频数统计表

分数段	频数	频率
80≤x＜85	100	0.2
85≤x＜90	x
90≤x＜95	160	y
95≤x＜100	120

根据图表提供的信息，解答下列问题：

（1）参加调查的同学有多少名？
（2）求表中x ， y的数值，并补全频数分布直方图；
（3）如果成绩在90分以上（含90分）为优秀，那么该市12000名学生中优秀的学生有多少人？

答案解析收藏纠错 + 选题

24. (2021七下·嘉兴期末) 比较 $\text{[math]}$ ×（a+1）与 $\text{[math]}$ +（a+1）的大小．
1. （1）尝试（用“＜”，“＝”或“＞”填空）：
  ①当a＝﹣2时， $\text{[math]}$ ×（a+1） $\text{[math]}$ +（a+1）
  
  ②当a＝2时， $\text{[math]}$ ×（a+1） $\text{[math]}$ +（a+1）
  
  ③当a＝ $\text{[math]}$ 时， $\text{[math]}$ ×（a+1） $\text{[math]}$ +（a+1）
2. （2）归纳：若a取不为零的任意实数， $\text{[math]}$ ×（a+1）与 $\text{[math]}$ +（a+1）有怎样的大小关系？试说明理由．
答案解析收藏纠错 + 选题
25. (2021七下·嘉兴期末) 某车行经营A ， B两种型号的电瓶车，已知A型车和B型车的进货价格分别为1500元和2500元．
1. （1）该车行去年A型车销售总额为8万元，今年A型车每辆售价比去年降低200元，若今年A型车的销售量与去年相同，则A型车销售额将比去年减少10%，求去年每辆A型车的售价．
2. （2）今年第三季度该车行计划用3万元再购进A ， B两种型号的电瓶车若干辆，问：
  ①一共有几种进货方案；
  
  ②在（1）的条件下，已知每辆B型车的利润率为24%，①中哪种方案利润最大，最大利润是多少？（利润＝售价﹣成本，利润率＝ $\text{[math]}$ ×100%）．
答案解析收藏纠错 + 选题
26. (2021七下·嘉兴期末) 如图1，把边长为b的正方形放在长方形ABCD中，其中正方形的两条边分别在AD ， CD上，已知AB＝a（a＜2b），BC＝4a ．
1. （1）请用含a、b的代数式表示阴影部分的面积；
2. （2）将另一长方形BEFG放入图1中得到图2，已知BE＝ $\text{[math]}$ a ， BG＝b；
  ①长方形AGPH的面积是长方形ECNM面积的6.5倍，求 $\text{[math]}$ 的值；
  
  ②若长方形PQMF的面积为2，求阴影部分的面积（用含b的代数式表示）．
答案解析收藏纠错 + 选题