 B .
B .  C .
C .  D .
D . 





甲采摘园的优惠方案是:游客进园需购买门票,采摘的草莓按售价的五折销售.
乙采摘园的优惠方案是:游客进园不需要购买门票,采摘的草莓按售价的七折销售;
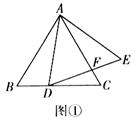
优惠期间,设某一位游客的草莓采摘量为 千克,在甲采摘园所需总费用为
元,且
,在乙采摘园所需总费用为
元,且
.其函数图象如图所示.
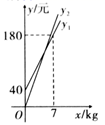


已知:如图①,过 外一点
作
的两条割线,一条交
于
、
点,另一条交
于
、
点.
求证: .
证明一:连接 、
,
∵ 和
为
所对的圆周角,∴_▲_.
又∵ ,∴_▲_,∴_▲_.
即 .
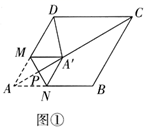
研究后发现,如图②,如果连接 、
,即可得到学习过的圆内接四边形
.那么或许割线定理也可以用圆内接四边形的性质来证明.请根据提示,独立完成证明二.
证明二:连接 、
,

| | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| | 4.0 | 3.18 | 2.48 | 2.06 | 2.07 | 2.53 | 3.23 |
操作中发现:“线段 的长度无需测量即可得到”.因为
与
满足关系式:.
①当 时,
;②当
时,
;
试判断:当 时,
的大小有无变化?请仅就图2的情形给出证明;
在旋转过程中,求出 的最大值.