
 B .
B .  C .
C .  D .
D . 
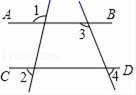



①以上化简步骤中,第步是进行分式的通分,通分的依据是;
②第步开始出现错误,这一步错误的原因是.
|
平均数 |
中位数 |
众数 |
最大值 |
最小值 |
方差 |
|
6.9 |
7.5 |
8 |
16 |
1 |
18.69 |
经过一年的“读书伴我行”阅读活动,某社区再次对这部分居民的年阅读量进行调查,并对收集的数据进行了整理、描述和分析,下面给出了部分信息.
a.居民的年阅读量统计表如下:
|
阅读量 |
2 |
4 |
5 |
8 |
9 |
10 |
11 |
12 |
13 |
16 |
21 |
|
人数 |
5 |
5 |
5 |
3 |
2 |
m |
5 |
5 |
3 |
7 |
n |
b.分组整理后的居民阅读量统计表、统计图如下:
|
组别 |
阅读量/本 |
频数 |
|
| | 15 |
| | | |
| | | 13 |
| | |

c.居民阅读量的平均数、中位数、众数、最大值、最小值、方差如下:
| 平均数 | 中位数 | 众数 | 最大值 | 最小值 | 方差 |
| 10.4 | 10.5 | q | 21 | 2 | 30.83 |
根据以上信息,回答下列问题:



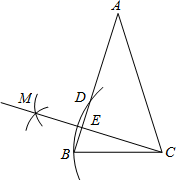
已知:如图,直线 与⊙O相切于
点,
,
为圆上不同于
的两点,连接
,
,
.
求证: .
小锐同学根据学习函数的经验,分别对函数 ,
随自变量
变化而变化的规律进行了探究.

下面是小锐同学的探究过程,请补充完整:
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| | 8.00 | 5.81 | 4.38 | 3.35 | 2.55 | 1.85 | 1.21 | 0.60 | 0.00 |
| | 0.00 | 0.90 | | 2.24 | 2.67 | 2.89 | 2.83 | 2.34 | 0.00 |
上表中 .(精确到0.1)

①当 ,
的长都大于
时,
长度的取值范围约是 ▲ ;(精确到0.1)
②继续在同一坐标系中画出所需的函数图象,判断点 ,
,
能否在以
为圆心的同一个圆上?(填“能”或“否”)
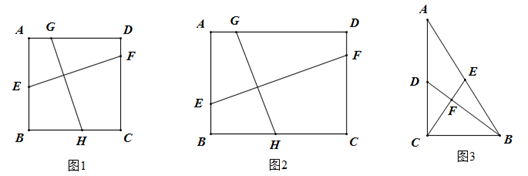
如图1,在正方形 中,点
,
,
,
分别在边
,
,
,
上,且
,则
;
如图2,在(1)的条件下,把“正方形 ”改为“矩形
,且
,
”其它条件不变,则
▲ ,证明你的结论;
如图3,在Rt 中,
,
,
,点
为
的中点,连接
,点
为
上一点,
,则
.