山东省烟台市蓬莱区2021-2022学年九年级下学期期中数学...

更新时间：2024-07-13 浏览次数：42 类型：期中考试

一、单选题

1. (2023七下·北辰期中) $\text{[math]}$ 的算术平方根是（）

A . 2 B . 4 C . ±2 D . ±4

答案解析收藏纠错 + 选题
2. (2022·平遥模拟) 下列图形均表示医疗或救援的标识，其中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022九下·蓬莱期中) 某个几何体的三视图如图所示，该几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022九下·蓬莱期中) 冠状病毒的直径约为80～120纳米，1纳米＝ $\text{[math]}$ 米，若用科学记数法表示110纳米，则正确的结果是（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
5. (2022九下·蓬莱期中) 已知一组数据5，4，3，4，9，关于这组数据的下列描述：①平均数是5，②中位数是4，③众数是4，④方差是4，其中正确的个数为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
6. (2024九下·射洪模拟) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两个实数根的平方和为12，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·费县模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点A为圆心，3为半径的圆与边 $\text{[math]}$ 相切于点D，与 $\text{[math]}$ ， $\text{[math]}$ 分别交于点E和点G，点F是优弧 $\text{[math]}$ 上一点， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 50° B . 48° C . 45° D . 36°

答案解析收藏纠错 + 选题
8. (2022九下·蓬莱期中) 如图，在△ABC中点D为△ABC的内心，∠A=60°，CD=2，BD=4．则△DBC的面积是（）

A . 4 $\text{[math]}$ B . 2 $\text{[math]}$ C . 2 D . 4

答案解析收藏纠错 + 选题
9. (2022九下·蓬莱期中) 如图，矩形 $\text{[math]}$ 的四个顶点分别在直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上．若直线 $\text{[math]}$ 且间距相等， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九下·蓬莱期中) 二次函数 $\text{[math]}$ 的部分图象如图所示，则下列选项错误的是（）

A . 若 $\text{[math]}$ ， $\text{[math]}$ 是图象上的两点，则 $\text{[math]}$ B . $\text{[math]}$ C . 方程 $\text{[math]}$ 有两个不相等的实数根 D . 当 $\text{[math]}$ 时，y随x的增大而减小

答案解析收藏纠错 + 选题

二、填空题

11. (2022九下·蓬莱期中) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是．

答案解析收藏纠错 + 选题
12. (2022九下·蓬莱期中) 已知关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 的解是非负数，则 $\text{[math]}$ 的取值范围为．

答案解析收藏纠错 + 选题
13. (2022九下·蓬莱期中) 如图，在直角坐标系中， $\text{[math]}$ OAB的顶点为O（0，0），A（4，3），B（3，0）.以点O为位似中心，在第三象限内作与 $\text{[math]}$ OAB的位似比为 $\text{[math]}$ 的位似图形 $\text{[math]}$ OCD，则点C的坐标为 .

答案解析收藏纠错 + 选题
14. (2022九下·蓬莱期中) 如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为1，△ABC经过平移后得到△A₁B₁C₁ ，若AC上一点P(1.2，1.4)平移后对应点为P₁、点P₁绕原点顺时针旋转180°，对应点为P₂ ，则点P₂的坐标为．

答案解析收藏纠错 + 选题
15. (2022九下·蓬莱期中) 如图，圆内接正六边形的边长为4，以其各边为直径作半圆，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
16. (2022九下·蓬莱期中) 如图，在正方形ABCD中，对角线AC与BD交于点O，点E在CD的延长线上，连接AE，点F是AE的中点，连接OF交AD于点G，若DE＝2cm，OF＝3cm，则点A到DF的距离为．

答案解析收藏纠错 + 选题

三、解答题

17. (2022九下·蓬莱期中) 先化再求代数式 $\text{[math]}$ 的值，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022九下·蓬莱期中) 某学校“校园主持人大赛”结束后，将所有参赛选手的比赛成绩（得分均为整数）进行整理，并分别绘制成扇形统计图和频数分布直方图．部分信息如下：
1. （1）本次比赛参赛选手共有人，扇形统计图中“79.5～89.5”这一范围的人数占总参赛人数的百分比为；
2. （2）补全图2频数分布直方图；
3. （3）成绩前四名是2名男生和2名女生，若从他们中任选2人作为该校文艺晚会的主持人，请用列举法（画树状图或列表）求所选取的这两名学生恰好是一男一女的概率．
答案解析收藏纠错 + 选题
19. (2022九下·蓬莱期中) 某服装专卖店计划购进 $\text{[math]}$ 两种型号的精品服装．已知2件A型服装和3件B型服装共需4600元；1件A型服装和2件B型服装共需2800元．
1. （1）求 $\text{[math]}$ 型服装的单价；
2. （2）专卖店要购进 $\text{[math]}$ 两种型号服装60件，其中A型件数不少于B型件数的2倍，如果B型打七五折，那么该专卖店至少需要准备多少货款？
答案解析收藏纠错 + 选题
20. (2022九下·蓬莱期中) 如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图，量得托板长 $\text{[math]}$ ，支撑板长 $\text{[math]}$ ，底座长 $\text{[math]}$ ，托板 $\text{[math]}$ 固定在支撑板顶端点 $\text{[math]}$ 处，且 $\text{[math]}$ ，托板 $\text{[math]}$ 可绕点 $\text{[math]}$ 转动，支撑板 $\text{[math]}$ 可绕点 $\text{[math]}$ 转动．（结果保留小数点后一位）（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离；
2. （2）为了观看舒适，在（1）的情况下，把 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 后，再将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转，使点 $\text{[math]}$ 落在直线 $\text{[math]}$ 上即可，求 $\text{[math]}$ 旋转的角度．
答案解析收藏纠错 + 选题
21. (2022九下·蓬莱期中) 如图，直线 $\text{[math]}$ 分别与x轴y轴交于A、B两点，反比例函数 $\text{[math]}$ 的图像与直线AB交于C，D两点点C的坐标为（2，n），连接OC， $\text{[math]}$ ．
1. （1）求反比例函数的表达式：
2. （2）若x轴上有一点P，使∠ODP=90°，求点P的坐标；
3. （3）若y₁≥y₂ ，请直接写出x的取值范围．
答案解析收藏纠错 + 选题
22. (2022九下·蓬莱期中) 如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB于点E，D是直径AB延长线上一点，且∠BCE＝∠BCD．
1. （1）求证：CD是⊙O的切线；
2. （2）若AD＝8， $\text{[math]}$ ＝ $\text{[math]}$ ，求CD的长．
答案解析收藏纠错 + 选题
23. (2022九下·蓬莱期中) 问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC、BC、CD之间的数量关系.
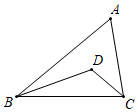
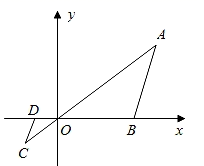
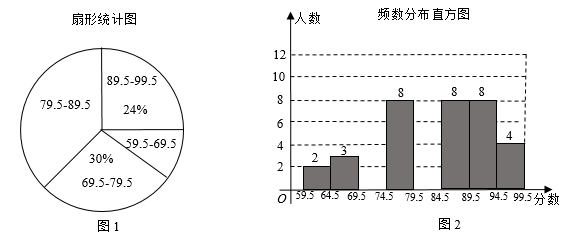
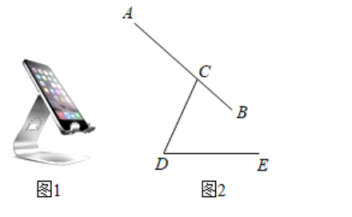
小吴同学探究此问题的思路是：将ΔBCD绕点D逆时针旋转90°到ΔAED处，点B、C分别落在点A、E处（如图②），易证点C、A、E在同一条直线上，并且ΔCDE是等腰直角三角形，所以CE＝ $\text{[math]}$ CD，从而得出结论：AC+BC＝ $\text{[math]}$ CD．

图①

图②

图③

图④

简单应用：
1. （1）在图①中，若AC＝ $\text{[math]}$ ，BC＝2 $\text{[math]}$ ，则CD＝.
2. （2）如图③，AB是⊙O的直径，点C、D在⊙O上，弧AD＝弧BD，若AB＝13，BC＝12，求CD的长.
3. （3）拓展延伸：
  如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m<n），求CD的长（用含m，n的代数式表示）.
答案解析收藏纠错 + 选题
24. (2022九下·蓬莱期中) 如图，抛物线 $\text{[math]}$ 与x轴交于点A(-2，0)，与反比例函数 $\text{[math]}$ 图象交于点B，过点B作BQ⊥y轴于点Q，BQ=1．
1. （1）求抛物线的表达式；
2. （2）若点P是抛物线对称轴上一点，当BP+OP的值最小时，求线段QP的长；
3. （3）若点M是平面直角坐标系内任意一点，在抛物线的对称轴上是否存在一点D，使得以A，B，D，M为顶点的四边形是菱形?若存在，请直接写出点D的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题