 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
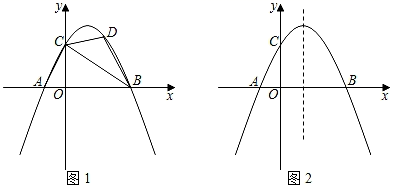
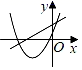
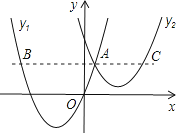
如图,抛物线y1=a(x+2)2-3与y2= (x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是( )
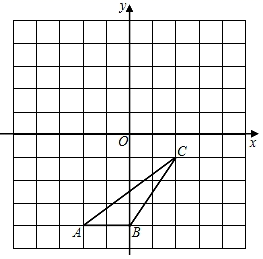
( 1 )画出△ABC关于点O的中心对称图形△A1B1C1 , 直接写出点C1的坐标为 ▲ .
( 2 )画出△ABC绕原点O逆时针旋转90°的△A2B2C2 , 直接写出点C2的坐标为 ▲ .
( 3 )若△ABC内一点P(m,n)绕原点O逆时针旋转180°的对应点为Q,则Q的坐标为 ▲ .
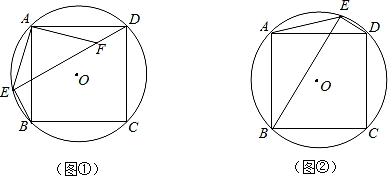
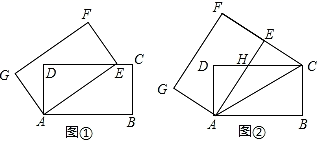
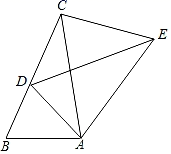
①求证: ADF≌
ABE;
②求证:DE﹣BE= AE.