湖北省武汉市洪山区2021年数学中考模拟试卷（5月）

更新时间：2021-10-30 浏览次数：169 类型：中考模拟

一、单选题

1. -2的相反数是（）

A . 2 B . -2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·厦门模拟) 式子 $\text{[math]}$ 在实数范围内有意义，则a的取值范围是（）

A . a≥﹣2 B . a≤﹣2 C . a＝0 D . a≥2

答案解析收藏纠错 + 选题
3. (2024八下·洪泽期中) 下列事件中，是必然事件的是（）

A . 任意买一张电影票，座位号是2的倍数 B . 13个人中至少有两个人生肖相同 C . 车辆随机到达一个路口，遇到红灯 D . 明天一定会下雨

答案解析收藏纠错 + 选题
4. (2022·兰溪模拟) 下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·洪山模拟) 如图，这是一个由5个完全相同的小正方体组成的立体图形，它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2021·洪山模拟) 袋中有三个小球，分别为1个红球和2个黄球，它们除颜色外完全相同.随机取出一个小球然后放回，则两次取出的小球颜色不同的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·洪山模拟) 已知A（m+1，y₁），B（3﹣m，y₂）两点在图象y＝ $\text{[math]}$ +2上，且y₁＞y₂ ，则m的取值范围是（）

A . m＜1 B . m＞3 C . 1＜m＜3 D . ﹣1＜m＜1或m＞3

答案解析收藏纠错 + 选题
8. (2021·洪山模拟) 用描点法画一次函数图象，在如表格中有一组数据错误，这组错误的数据是（）

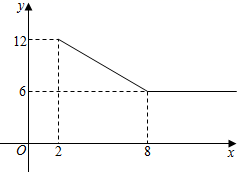
x

﹣2

﹣1

1

2

y

12

11

10

8

A . （﹣2，12） B . （﹣1，11） C . （1，10） D . （2，8）

答案解析收藏纠错 + 选题
9. (2021·洪山模拟) 如图，已知△ABC内接于⊙O，AB＝AC，与AC交于点E，连接CD并延长与⊙O过点A的切线交于点F，⊙O的半径为2，则图中阴影部分的面积为（）

A . $\text{[math]}$ ﹣ $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ ﹣ $\text{[math]}$ D . 1﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·洪山模拟) 在平面直角坐标系中，反比例函数y＝ $\text{[math]}$ 的图象经过（a，m+2 $\text{[math]}$ ），（b，m），则代数式 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . ﹣ $\text{[math]}$ C . 2 D . ﹣3

答案解析收藏纠错 + 选题

二、填空题

11. (2022八下·临淄期中) $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题
12. (2021·洪山模拟) 某车间20名工人日加工零件数如表所示：这些工人日加工零件数的中位数是.

日加工零件数

4

5

6

7

8

人数

2

6

5

4

3

答案解析收藏纠错 + 选题
13. (2021·洪山模拟) 分式方程 $\text{[math]}$ 的解是.

答案解析收藏纠错 + 选题
14. (2021·洪山模拟) 在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1，2号楼进行测高实践，测得1号楼顶部E的俯角为67°，测得2号楼顶部F的俯角为40°，此时航拍无人机的高度为60米，已知1号楼的高度为20米，且EC和FD分别垂直地面于点C和D，点B为CD的中点，则2号楼的高度为（结果精确到0.1）（参考数据sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）

答案解析收藏纠错 + 选题
15. (2021·洪山模拟) 已知抛物线y＝ax²+bx+c（a，b，c是常数，且a≠0）与x轴相交于点A，B（点A在点B左侧），其中点A（﹣1，0），C（0，c），其中2≤c≤3，对称轴为直线x＝1，①2a+b＝0；②当x≥3时，y＜0 ；③二次函数的最大值的最小值为4；④﹣1≤a≤﹣ $\text{[math]}$ .则其中正确结论的序号为.

答案解析收藏纠错 + 选题
16. (2021·洪山模拟) 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”，已知正方形ABCD的边长为4dm，则图2中h的值为dm.

答案解析收藏纠错 + 选题

三、解答题

17. (2023七下·天津市期末) 解不等式组 $\text{[math]}$
请结合题意填空，完成本题的解答．
1. （1）解不等式①，得；
2. （2）解不等式②，得；
3. （3）把不等式①和②的解集在数轴上表示出来：
4. （4）原不等式组的解集为．
答案解析收藏纠错 + 选题
18. (2021·洪山模拟) 如图，AB⊥AD，CD⊥AD，∠1＝∠2，求证：DE∥AF

答案解析收藏纠错 + 选题
19. (2021·洪山模拟) “保护环境，人人有责”，为了了解某市的空气质量情况，某校环保兴趣小组，随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）.
请你根据图中提供的信息，解答下列问题：
1. （1）补全条形统计图；
2. （2）估计该市这一年（365天）空气质量达到“优”和“良”的总天数；
3. （3）计算随机选取这一年内的某一天，空气质量是“优”的概率.
答案解析收藏纠错 + 选题
20. (2021·洪山模拟) 如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫格点，△ABC的顶点都在格点上（保留作图连线痕迹），并回答问题.

（ 1 ）在BC的右边找格点D，连AD，使AD平分∠BAC.

（ 2 ）若AD与BC交于E，直接写出 $\text{[math]}$ 的值.

（ 3 ）找格点F，连EF，使EF⊥AB于H.

（ 4 ）在AC上找点G，连EG，使EG∥AB.

答案解析收藏纠错 + 选题
21. (2021·硚口模拟) 如图，AB是⊙O的直径，AC交⊙O于点D，点E时弧AD的中点，BE交AC于点F，BC＝FC.
1. （1）求证：BC是⊙O的切线；
2. （2）若BF＝3EF，求tan∠ACE的值.
答案解析收藏纠错 + 选题
22. (2021·洪山模拟) 某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类；B类杨梅深加工后再销售，A类杨梅的包装成本为1万元/吨，根据市场调查，平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图，B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s＝12+3t，平均销售价格为9万元/吨，
1. （1）直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式；
2. （2）第一次，该公司收购了20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的总利润为w万元，求w关于x的函数关系式；
3. （3）第二次，该公司准备投入132万元资金，请设计一种经营方案，使公司获得最大利润，并求出最大利润.
答案解析收藏纠错 + 选题
23. (2021·洪山模拟) 在 $\text{[math]}$ 中，∠BAC＝90°，AB＝AC，D为BC的中点，F，E是AC上两点，连接BE、DF交于 $\text{[math]}$ 内的一点G，且∠EGF＝45°.
1. （1）如图1，若AE＝3CE＝3，求BG的长；
2. （2）如图2，若E为AC上任意一点，连接AG，求 $\text{[math]}$ ；
3. （3）若E为AC的中点，求EF：FD的值.
答案解析收藏纠错 + 选题
24. (2021·洪山模拟) 已知抛物线y＝ax²+bx﹣3经过A（﹣1，0），且与x轴右侧交于B点，对称轴为直线x＝1，与y轴交于C点.
1. （1）求抛物线的解析式；
2. （2）如图1，过点C作直线l∥x轴交抛物线于点D，点P在抛物线上，且∠DCP＝∠ACO，求点P的坐标；
3. （3）如图2，直线y＝kx+b（k≠b）交抛物线于M、N两点，NH⊥x轴于点H，HQ与MN相交于点Q，求点Q的横坐标.
答案解析收藏纠错 + 选题