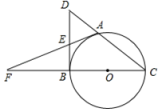
B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
| 体温(单位:℃) | 36.2 | 36.3 | 36.5 | 36.7 | 36.8 |
| 人数 | 8 | 10 | 7 | 13 | 12 |
则这50名学生体温的众数和中位数分别是( )





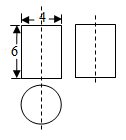

(结果精确到0.1米.参考数据:sin53°≈0.798,cos53°≈0.602,tan53°≈1.327.)