 B .
B .  C .
C .  D .
D . 

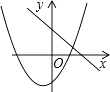 B .
B . 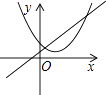 C .
C . 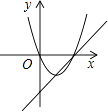 D .
D . 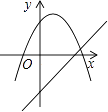




|
售价x(元) |
... |
70 |
65 |
60 |
... |
|
销售量y(个) |
... |
300 |
350 |
400 |
... |

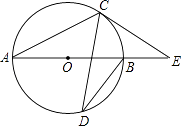
①求∠OCE的度数;
②若⊙O的半径为2 ,求线段EF的长.

