 B .
B .  C .
C .  D .
D . 
如图,⑴以点O为圆心,适当长为半径画弧,交OA 于点M , 交OB 于点N;
⑵分别以点M , N为圆心,大于 MN 的长为半径画弧,两弧在∠AOB的内部相交于点C;
⑶画射线OC . 射线OC即为所求. 其中的道理是,作出△OMC≌△ONC , 根据全等三角形的性质,得到∠AOC=∠BOC , 进而得到OC是∠AOB的平分线. 其中,△OMC≌△ONC的依据是( )
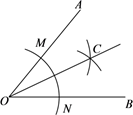





三角形中边与角之间的不等关系
学习了等腰三角形,我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边所对的角之间的大小关系怎样呢?大边所对的角也大吗?下面是奋进小组的证明过程.

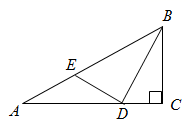
如图1,在△ABC中,已知AB>AC>BC .
求证:∠C>∠B>∠A .
证明:如图2,将△ABC折叠,使边AC落在AB上,
点C落在AB上的点C′处,折痕AD交BC于点D .
则∠A C′D=∠C .
∵∠A C′D=∠B+∠BDC′(依据1)
∴∠A C′D>∠B
∴∠C>∠B(依据2)
如图3,将△ABC折叠,使边CB落在CA上,点B落在CA上的点B′处,折痕CE交AB于点E . 则∠CB′E=∠B .
∵∠CB′E=∠A+∠AEB′
∴∠CB′E>∠A
∴∠B>∠A
∴∠C>∠B>∠A .
归纳总结:利用轴对称的性质可以把研究边与角之间的不等问题,转化为较大量的一部分与较小量相等的问题,这是几何中研究不等问题是常用的方法.
类似地,应用这种方法可以证明“在一个三角形中,大角对大边,小角对小边”的问题.如图1,已知△ABC中,∠C>∠B>∠A . 求证:AB>AC>BC . 下面是智慧小组的证明过程(不完整).

证明:如图2,在∠BCA的内部,作∠BCF=∠B , CF交AB于点F .
则CF=BF(依据3)
在△ACF中,AF+CF>AC ,
∴AF+BF>AC ,
∴AB>AC;…
①上述材料中依据1,依据2,依据3分别指什么?
依据1:;
依据2:;
依据3:.
A. 转化思想 B. 方程思想 C. 数形结合思想
①在△ABC中,AB>BC , 则∠A>∠B;
②在△ABC中,AB>BC>AC , ∠C=89°,则△ABC是锐角三角形;
③Rt△ABC中,∠B=90°,则最长边是AC;
④在△ABC中,∠A=55°,∠B=70°,则AB=BC .
如图2,将三角尺ABC和三角尺DEF如图摆放,连接CF , 交AB于点G , 请你证明CG= FG;