湖北省武汉市武汉六初、六中上智2021-2022学年九年级上...

更新时间：2021-11-15 浏览次数：142 类型：月考试卷

一、单选题

1. (2022九上·岳麓月考) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . 三角形 B . 等边三角形 C . 平行四边形 D . 菱形

答案解析收藏纠错 + 选题
2. (2021九上·武汉月考) 一元二次方程2x²＝x﹣3的二次项系数和常数项分别是（　　）

A . 2，﹣1 B . 2，3 C . ﹣1，3 D . ﹣1，2

答案解析收藏纠错 + 选题
3. (2021九上·武汉月考) 已知m是一元二次方程x²﹣4x+1＝0的一个根，则2021﹣m²+4m的值为（　　）

A . ﹣2021 B . 2021 C . 2020 D . 2022

答案解析收藏纠错 + 选题
4. (2021九上·武汉月考) 抛物线y＝﹣2x²经过平移后得到y＝﹣2（x+3）²﹣4，其平移方法是（）

A . 向右平移3个单位，再向下平移4个单位 B . 向右平移3个单位，再向上平移4个单位 C . 向左平移3个单位，再向下平移4个单位 D . 向左平移3个单位，再向上平移4个单位

答案解析收藏纠错 + 选题
5. (2022九上·岳麓月考) 如图，在△ABC中，∠B＝55°，∠ACB＝30°，将△ABC绕点C顺时针旋转n度（0＜n＜180）得到△EDC，若CE∥AB，则n的值为（　　）

A . 65 B . 90 C . 95 D . 125

答案解析收藏纠错 + 选题
6. (2021九上·武汉月考) 某种细胞分裂，一个细胞经过两轮分裂后，共有a个细胞，设每轮分裂中平均一个细胞分裂成x个细胞，那么可列方程为（　　）

A . x²＝a B . （1＋x）²＝a C . 1＋x＋x²＝a D . x＋x²＝a

答案解析收藏纠错 + 选题
7. (2021九上·武汉月考) 已知二次函数y＝3（x﹣1）²+h的图象上有三点，A（﹣0.5，y₁），B（2.5，y₂），C（3，y₃），则y₁ ， y₂ ， y₃的大小关系为（　　）

A . y₁＝y₂＜y₃ B . y₁＜y₂＜y₃ C . y₁＜y₂＝y₃ D . y₃＜y₁＝y₂

答案解析收藏纠错 + 选题
8. (2022九上·岳麓月考) 在同一平面直角坐标系中，一次函数y＝kx﹣1与二次函数y＝kx²＋3的大致图象可以是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2021九上·武汉月考) 在平面直角坐标系中，一个蜘蛛最初在点A（p，0）（p是常数，且p＞1），第一次爬到射线OA绕O点逆时针旋转60°方向上的A₁点，且OA₁＝pOA；第二次爬到射线OA₁绕O点逆时针旋转60°方向上的A₂点，且OA₂＝pOA₁；…；第2021次爬行到A₂₀₂₁点的坐标是（　　）

A . （p²⁰²¹ ， 0） B . $\text{[math]}$ C . （﹣p²⁰²¹ ， 0） D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021九上·武汉月考) 当m≤x≤m+1时，函数y＝x²﹣4|x|+2的最大值为2，则m满足的条件为（　　）

A . ﹣1＜m≤0 B . m＝﹣4或3或﹣1≤m≤0 C . m＝﹣4或﹣1＜m≤0 D . m＝﹣4或3

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·城厢开学考) 在平面直角坐标系中，点P（﹣3，1）关于坐标原点中心对称的点P′的坐标是.

答案解析收藏纠错 + 选题
12. (2021九上·武汉月考) 抛物线y=-x²+2x+2的顶点坐标是．

答案解析收藏纠错 + 选题
13. (2021九上·武汉月考) 二次函数y＝kx²﹣3x＋1的图象与x轴有公共点，则常数k的取值范围是.

答案解析收藏纠错 + 选题
14. (2021九上·武汉月考) 飞机着陆后滑行的距离y（单位：m）关于滑行时间t（单位：s）的函数解析式是 $\text{[math]}$ ，飞机着陆至停下来共滑.

答案解析收藏纠错 + 选题
15. (2021九上·武汉月考) 已知二次函数y＝ax²+bx+c（a≠0）的的部分图象如图，图象经过（﹣1，0），对称轴为x＝2.下列4个结论：①4a+b＝0；②9a+c＞3b；③一元二次方程cx²+bx+a＝0两根为﹣1和 $\text{[math]}$ ；④不等式a（x+1）（x﹣5）＜﹣3的解集满足x＜﹣1或x＞5.其中正确的结论序号是.

答案解析收藏纠错 + 选题
16. (2021九上·武汉月考) 如图，在△ABC中，∠BAC＝120°，AB+AC＝a（a＞0），将CB绕C顺时针旋转120°得CD，当DA长的最小值为 $\text{[math]}$ 时，a的值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·武汉月考) 解方程：
1. （1） x²+2x＝0；
2. （2） 4x²﹣x﹣9＝0.
答案解析收藏纠错 + 选题
18. (2021九上·武汉月考) 如图，利用一面墙（墙的长度不限），用 $\text{[math]}$ 长的篱笆，怎样围成一个面积为 $\text{[math]}$ 的矩形场地？

答案解析收藏纠错 + 选题
19. (2021九上·武汉月考) 已知关于x的一元二次方程x²﹣2kx+k²+k＝0有实数根.
1. （1）求k的取值范围；
2. （2）设此方程的两个根分别为x₁ ， x₂ ，若x₁²+x₂²+3x₁x₂＝6，求k的值.
答案解析收藏纠错 + 选题
20. (2021九上·武汉月考) 如图所示，在由边长为1的小正方形组成的正方形网格中建立平面直角坐标系，格点 $\text{[math]}$ ABC的顶点坐标分别为A（1，4）、B（6，4）、C（2，0），请仅用无刻度直尺，在给定的网格中依次完成下列作图（要求保留必要的作图痕迹），并回答下列问题：

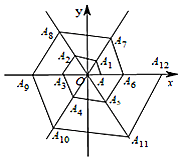
（ 1 ）在AB上找点E，使∠ACE＝45°.

（ 2 ）点A关于直线BC的对称点为D，在BD上找点F，使BF＝BE.

（ 3 ）将线段AC绕点Q逆时针方向旋转90°得到线段BH，使点C的对应点为点B，画出线段BH，并写出点Q的坐标.

答案解析收藏纠错 + 选题
21. (2021九上·武汉月考) 如图，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于A、B两点.
1. （1）直接写出当y₁＜y₂时，自变量x的取值范围.
2. （2）点C在抛物线上，点D在直线AB上，当四边形AODC是平行四边形时，求点C的横坐标.
答案解析收藏纠错 + 选题
22. (2021九上·朝阳期中) 某宾馆有50间相同的客房，当房间的定价为每天180元时，房间会全部住满.统计表明：当房价每上调10元时，就会有一个房间空闲，宾馆需对有客人居住的房间每天支出20元的各种费用.设该宾馆房价上调x元（x为10的正整数倍）时，相应的住房数为y间.
1. （1）求y与x的函数关系式.
2. （2）房价为多少时，宾馆的利润最大？最大利润是多少？
3. （3）若老板决定每住进去一间房就捐出a元（0＜a≤40）给当地福利院，同时要保证房间定价在180元至360元之间波动时（包括两端点），利润随x的增大而增大，求a的取值范围.
答案解析收藏纠错 + 选题
23. (2021九上·武汉月考) 在△ABE和△CDE中，∠ABE＝∠DCE＝90°，AB＝BE，CD＝CE.
1. （1）连接AD、BC，点M、N分别为AD、BC的中点，连接MN，
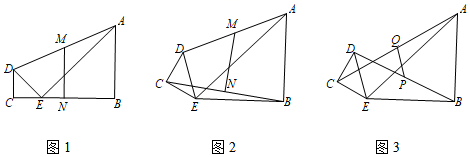
  ①如图1，当B、E、C三点在一条直线上时，MN与BC关系是 .
  
  ②如图2，当等腰Rt△CDE绕点E顺时针旋转时，①中的结论还成立吗？如果成立，请证明你的结论；如果不成立，请说明理由.
2. （2）如图3，当等腰Rt△CDE绕点E顺时针旋转时，连接AC、BD，点P、Q分别为BD、AC的中点，连接PQ，若AB＝13，CD＝5，则PQ的最大值时，此时以A、B、C、D为顶点的四边形的面积为 .
答案解析收藏纠错 + 选题
24. (2021九上·武汉月考) 已知抛物线与x轴交于点A、点B，与y轴交于点C（0，3），顶点坐标（﹣2，﹣1）.
1. （1）求抛物线的解析式.
2. （2）如图1，点D在第二象限的抛物线上，且∠CBO＝∠CBD，求点D的坐标.
3. （3）如图2，将抛物线平移至顶点与原点重合得到新抛物线，M、N在新抛物线上且M在N的左侧，过M、N的两条直线与抛物线均有唯一的公共点，且两条直线交于点E，过E作EF∥y轴交MN于F，交抛物线于G，求证：G是EF中点.
答案解析收藏纠错 + 选题