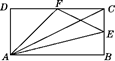
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

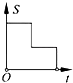 B .
B . 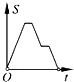 C .
C . 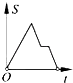 D .
D . 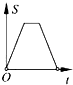

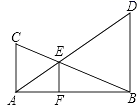


⑴画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1;
⑵以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2 , 请在网格中画出△A2B2C2 .
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为 ,依此类推,排在第n位的数称为第n项,记为
.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示 .如:数列1,3,9,27,…为等比数列,其中
,公比为
.则:
所以: ,
,
,…
由此可得: (用
和q的代数式表示).
请解答下列问题: