| 摸球试验的次数 | 100 | 200 | 500 | 1000 |
| 摸出白球的次数 | 21 | 39 | 102 | 199 |
根据列表可以估计出n的值为( )
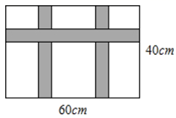
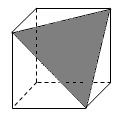
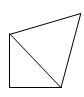 B .
B .  C .
C . 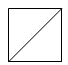 D .
D . 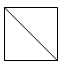
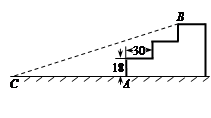
(参考数据: )

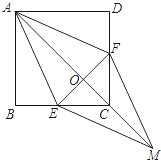
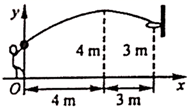
小颖发现某座房屋的侧面是一种特殊的五边形,她决定好好研究一下它的特点,并计算它的面积.
(问题探究)
定义:如图(1),我们把满足 的五边形
叫做屋形.其中
叫做脊,
叫做腰,
叫做底.
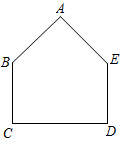
性质:
边:屋形的腰相等,脊相等;
角:①屋形腰与底的夹角相等;②脊与腰的夹角相等;
对角线:①
②屋形有两组对角线分别相等,且其中一组互相平分.
对称性:屋形是以底的垂直平分线为对称轴的轴对称图形;
已知:如图,五边形 是屋形.
求证:
证明:

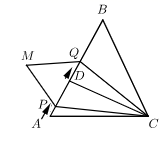
解答下列问题:
