山东省青岛市市南区2020-2021学年九年级上学期期末数学...

更新时间：2021-12-17 浏览次数：143 类型：期末考试

一、单选题

1. (2022九下·长沙月考) 如图的一个几何体，其左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021九上·汕尾期末) 一个不透明的口袋中装有10个黑球和若干个白球，小球除颜色外其余均相同，从中随机摸出一球记下颜色，再放回袋中，不断重复上述过程，一共摸了150次，其中有50次摸到黑球，由此估计口袋中白球的个数约为（）

A . 10个 B . 20个 C . 30个 D . 40个

答案解析收藏纠错 + 选题
3. (2020九上·青岛期末) 已知关于x的方程x²+2x+k＝0有实数根，则k的值为（）

A . k≤1 B . k＜1 C . k≥1 D . k＞1

答案解析收藏纠错 + 选题
4. (2020九上·青岛期末) 反比例函数y $\text{[math]}$ 的图象上有三个点，分别是（x₁ ， y₁）（x₂ ， y₂）（x₃ ， y₃），若x₁＜0＜x₂＜x₃ ，则y₁ ， y₂ ， y₃的大小关系是（）

A . y₁＜y₂＜y₃ B . y₂＜y₁＜y₃ C . y₃＜y₁＜y₂ D . y₂＜y₃＜y₁

答案解析收藏纠错 + 选题
5. (2023九上·东阳期中) 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），则下列结论中正确的是（）

A . AB²＝AP²+BP² B . BP²＝AP•BA C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·青岛期末) 将函数y＝（x+1）²﹣4的图象先向右平移2个单位长度，再向上平移4个单位长度，则得到的函数解析式为（）

A . y＝（x﹣1）² B . y＝（x﹣1）²﹣8 C . y＝（x+3）² D . y＝（x+3）²﹣8

答案解析收藏纠错 + 选题
7. (2020九上·青岛期末) 如图，在菱形ABCD中，E是AD边的中点，连接BE交AC于点F，连接DF，下列四个结论：①△AEF∽△CBF，②CF＝2AF，③DF＝DC，④2S_{四边形CDEF}＝5S_△ABF ，其中正确正确的结论有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
8. (2020九上·青岛期末) 在同一平面直角坐标系中，二次函数y＝ax²+bx，一次函数y＝ax+b和反比例函数y $\text{[math]}$ 的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. (2020九上·青岛期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
10. (2020九上·青岛期末) 随着国家“惠民政策”的陆续出台，为了切实让老百姓得到实惠，某种药品原价198元/瓶，经过连续两次降价后，现仅售78元/瓶，假定两次降价的百分率相同，设该种药品平均每次降价的百分率为x，则列出的关于x方程为．

答案解析收藏纠错 + 选题
11. (2020九上·青岛期末) 如图，在平面直角坐标系中，△ABC的三个顶点分别在格点上，其中A（3，2）、B（1，﹣1）、C（4，0）．以点B为位似中心，在y轴的右侧，将△ABC放大为原来的2倍，得到△A₁B₁C₁则点A的对应点A₁的坐标为．

答案解析收藏纠错 + 选题
12. (2020九上·青岛期末) 在△ABC中，AB＝5，BC＝8，AD是BC边上的高，AD＝4，则tanC＝．

答案解析收藏纠错 + 选题
13. (2020九上·青岛期末) 已知线段a的长度为11，现从1～10这10条整数线段中任取两条，能和线段a组成三角形的概率为．

答案解析收藏纠错 + 选题
14. (2021九上·青岛期中) 如图，在矩形ABCD中，AB＝4，∠ACB＝30°，E，F分别为对角线AC与边CD上的点，且AE＝CF，则BE+BF的最小值为．

答案解析收藏纠错 + 选题

三、解答题

15. (2022九上·青岛开学考) 已知：∠A和∠A一边上的点B．求作：▱ABCD，满足∠A是它的一个内角，且对角线BD⊥AD．

答案解析收藏纠错 + 选题
16. (2020九上·青岛期末)
1. （1）解方程：2x²+4x﹣3＝0；
2. （2）计算：sin²45°+tan60°•cos30°．
答案解析收藏纠错 + 选题
17. (2020九上·青岛期末) 为落实“十个一“活动，学校组建了多个志愿者服务队，小盖和小吕通过做游戏决定谁优先选择服务队，游戏规则：两人各掷一次质地均匀的骰子，如果掷出的点数之和是小于7的偶数，由小盖优先选择服务队；如果掷出的点数之和是大于6的奇数，由小吕优先选择服务队．请你利用画树状图或列表的方法，判断这个游戏对双方是否公平．

答案解析收藏纠错 + 选题
18. (2020九上·青岛期末) 小颖的数学学习日记：x月x日：测量旗杆的高度．
1. （1）今天上午王老师要带我们去操场测量旗杆的高度，昨天我们小组设计了一个方案，方案如下：小亮拿着标杆垂直于地面放置，我和小聪用卷尺测量标杆、标杆的影长和旗杆的影长，如图1所示，标杆AB＝a，影长BC＝b，旗杆的影长DF＝c，则可求得旗杆DE的高度为．
2. （2）但今天测量时，阴天没有阳光，就不能用以上的方案了．如图2所示，王老师将升旗用的绳子拉直，使绳子的底端G刚好触到地面，用仪器测得绳子与地面的夹角为37°，然后又将绳子拉到一个0.5米高的平台上，拉直绳子使绳子上的H点刚好触到平台，剩余的绳子长度为5米，此时测得绳子与平台的夹角为54°，利用这些数据能求出旗杆DE的高度吗？（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75；sin54°≈0.8，cos54°≈0.58，tan54°≈1.45）请你回答小颖的问题．若能，请求出旗杆的高度；若不能，请说明理由．
答案解析收藏纠错 + 选题
19. (2020九上·青岛期末) 在“学习一项体育技能”活动中，小明作为学生代表去观看“青岛黄海足球队”的训练．他看到队员们在做掷界外球训练，甲球员要将足球掷给离他7.5米远的乙球员，掷出足球的运行轨还是一条抛物线，足球行进的高度y（米）与水平距离x（米）之间的关系如图所示，足球出手时离地面的高度为2米，在距离甲球员4米处达到最大高度3.6米．若不计其他因素，身高1.85米的乙球员要能触到足球，他垂直起跳的高度至少要达到多少米？

答案解析收藏纠错 + 选题
20. (2020九上·青岛期末) 如图，直线y＝kx+3与x轴、y轴分别交于点B、C，与反比例函数y $\text{[math]}$ 交于点A、D，过D做DE⊥x轴于E，连接OA，OD，若A（﹣2，n），S_△OAB：S_△ODE＝1：2．
1. （1）求反比例函数的表达式；
2. （2）求点C的坐标．
答案解析收藏纠错 + 选题
21. (2020九上·青岛期末) 已知：如图，在平行四边形ABCD中，E、F分别为AB、CD的中点，G、H分别为DE、BF的中点．
1. （1）试判断四边形EHFG的形状，并证明；
2. （2）若∠ABC＝90°，试判断四边形EHFG的形状并加以并证明．
答案解析收藏纠错 + 选题
22. (2020九上·青岛期末) 某快餐店新推出一种外卖，每份的成本为20元，推出后每份售价为50元，每月可售出200份，经过试卖发现，该外卖每份售价每降价1元，每月可多卖出10份，由于制作能力有限，每月最多制作该外卖350份．设该外卖每份售价x元（x≤50），每月的销售利润为w元．
1. （1）求w与x之间的函数关系式；
2. （2）该外卖每份售价多少元时，每月的销售利润最大？最大利润是多少？
3. （3）该外卖每份售价在什么范围时，每月的销售利润不低于4000元．
答案解析收藏纠错 + 选题
23. (2020九上·青岛期末) 问题提出：如图1，D、E分别在△ABC的边AB、AC上，连接DE，已知线段AD＝a，DB＝b，AE＝c，EC＝d，则S_△ADE ， S_△ABC和a，b，c，d之间会有怎样的数量关系呢？
1. （1）问题解决：探究一：
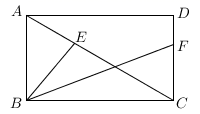
  ①看到这个问题后，我们可以考虑先从特例入手，找出其中的规律．如图2，若DE∥BC，则∠ADE＝∠B，且∠A＝∠A，所以△ADE∽△ABC，可得比例式： $\text{[math]}$ 而根据相似三角形面积之比等于相似比的平方．可得 $\text{[math]}$ ．根据上述这两个式子，可以推出： $\text{[math]}$ ．
  
  ②如图3，若∠ADE＝∠C，上述结论还成立吗？若成立，请写出证明过程；着不成立，请说明理由．
2. （2）探究二：回到最初的问题，若图1中没有相似的条件，是否仍存在结论： $\text{[math]}$ ？方法回顾：两个三角形面积之比，不仅可以在相似的条件下求得，当两个三角形的底成高具有一定的关系时，也可以解决．如图4，D在△ABC的边上，做AH⊥BC于H，可得： $\text{[math]}$ ．借用这个结论，请你解决最初的问题．
  延伸探究：
  
  ①如图5，D、E分别在△ABC的边AB、AC反向延长线上，连接DE，已知线段AD＝a，AB＝b，AE＝c，AC＝d，则 $\text{[math]}$ ．
  
  ②如图6，E在△ABC的边AC上，D在AB反向延长线上，连接DE，已知线段AD＝a，AB＝b，AE＝c，AC＝d， $\text{[math]}$ ．
3. （3）结论应用：如图7，在平行四边形ABCD中，G是BC边上的中点，延长GA到E，连接DE交BA的延长线于F，若AB＝5，AG＝4，AE＝2，▱ABCD的面积为30，则△AEF的面积是．
答案解析收藏纠错 + 选题
24. (2020九上·青岛期末) 已知：如图，在△ABC中，AB＝AC＝5cm，BC＝8cm，AD⊥BC，垂足为D，F为AD中点．点P从点B出发，沿BC向点C匀速运动，速度为1cm/s同时，点Q从点A出发，沿AB向点B匀速运动，速度为1cm/s；点E为点P关于AD的对称点．连接PQ、FQ、EF、AE．设运动时间为t（s）（0＜t＜4），解答下列问题：
1. （1）当PQ∥AE时，求t的值；
2. （2）设四边形AEPQ的面积为y（cm²），试确定y与t的函数关系式；
3. （3）在运动过程中，是否存在某一时刻t，使∠DFE＝∠AFQ？若存在，求出t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题