湖南省长沙市雅礼教育集团2021-2022学年九年级下学期第...

更新时间：2024-07-13 浏览次数：112 类型：月考试卷

一、单选题

1. (2021七上·兰陵期中) 四个有理数-3、-1、0、1，其中最小的是（）

A . -3 B . -1 C . 0 D . 1

答案解析收藏纠错 + 选题
2. (2022九下·长沙月考) 截止到2021年10月24日，国庆档电影《长津湖》累计票房超过了约5253000000元，正式跻身中国电影历史票房前三名，将5253000000用科学记数法表示为（）

A . 5.253×10⁹ B . 5.253×10³ C . 52.53×10⁸ D . 0.5253×10¹⁰

答案解析收藏纠错 + 选题
3. (2023七下·砀山期末) 下列图形中，不是轴对称图形的是（）

A . 平行四边形 B . 等腰三角形 C . 圆 D . 菱形

答案解析收藏纠错 + 选题
4. (2022九下·长沙月考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九下·长沙月考) 不等式组 $\text{[math]}$ 的解集在数轴上可以表示为（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2022九下·长沙月考) 如图，Rt△ABC中，∠ABC=90°，边AB在x轴上，以O为位似中心，作△A₁B₁C₁与△ABC位似，若C（4，6）的对应点C₁（2，3），则B₁的坐标为（）

A . （1，0） B . （ $\text{[math]}$ ， 0） C . （2，0） D . （2，1）

答案解析收藏纠错 + 选题
7. (2022九下·长沙月考) 如图的一个几何体，其左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2023·大朗模拟) 端午节那天，欢欢回家看到桌上有一盆粽子，其中豆沙馅粽子1个，板栗馅粽子2个，五花肉馅粽子1个，这些粽子除馅外无其它差别.欢欢从盆中随机取出1个粽子，是豆沙馅粽子的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九下·长沙月考) 小明在某次投篮中刚好把球打到篮板的点D处后进球，已知小明与篮框底的距离BC＝5米，眼睛与地面的距离AB＝1.7米，视线AD与水平线的夹角为∠α，已知tanα＝ $\text{[math]}$ ，则点D到地面的距离CD是（）

A . 2.7米 B . 3.0米 C . 3.2米 D . 3.4米

答案解析收藏纠错 + 选题
10. (2022·马鞍山模拟) 如图1，在平行四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，动点P从点A出发，以每秒1个单位的速度沿线段AB运动到点B停止，同时动点Q从点B出发，以每秒4个单位的速度沿折线 $\text{[math]}$ 运动到点D停止.图2是点P、Q运动时， $\text{[math]}$ 的面积S与运动时间t函数关系的图象，则a的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 6 D . 12

答案解析收藏纠错 + 选题

二、填空题

11. (2022九下·长沙月考) 若 $\text{[math]}$ 有意义，则x的取值范围为.

答案解析收藏纠错 + 选题

12. (2022九下·长沙月考) 长沙地铁6号线即将试运行，为了解学校同学每周乘坐地铁出行的次数，校园小记者随机调查了50名同学，得到如下统计表：

次数	7次及以上	6	5	4	3次及以下
人数	4	5	11	24	6

这次调查中的中位数是.

答案解析收藏纠错 + 选题

13. (2022九下·长沙月考) 已知方程组 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2022九下·长沙月考) 如图，矩形ABCD的两条对角线相交于点O，已知∠AOD=120°，AB=2cm，则矩形对角线BD的长为cm.

答案解析收藏纠错 + 选题
15. (2022九下·长沙月考) 如图，在⊙O中，弦AB的长为 $\text{[math]}$ ，圆心到弦AB的距离为1，则∠BOC的度数为.

答案解析收藏纠错 + 选题
16. (2022九下·长沙月考) 如图，正比例函数 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象交于A，B两点，BC//x轴，AC//y轴，则S_△ABC=.

答案解析收藏纠错 + 选题

三、解答题

17. (2022九下·长沙月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2022九下·长沙月考) 先化简，再求值： $\text{[math]}$ ，其中a=2022.

答案解析收藏纠错 + 选题
19. (2022九下·长沙月考) 阅读下面内容，解答后面的问题.
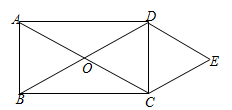
题目：尺规作图：如图1，已知线段MN（长度等于a），求作一个一条边长等于a，且有一个角为30°的直角三角形.

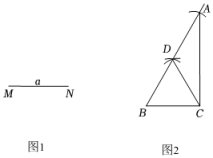
小雅同学的解答作图方法如下：

①作线段BC=MN；

②分别以点B、C为圆心，以线段BC长为半径画弧，两弧相交于点D；

③连结BD、CD；

④延长BD到A，使DA=BC；

⑤连结AC.

则△ABC就是所求作的直角三角形.

根据小雅同学作图方法：
1. （1）请你证明△ABC是直角三角形；
2. （2）若CD=2，求AC的长.
答案解析收藏纠错 + 选题

20. (2023九下·长沙月考) 北京冬奥会已于2022年2月4日至20日举行，北京成为奥运史上第一个举办过夏季奥运会和冬季奥运会的城市.为了了解学校学生对于北京冬奥会的了解情况，进行了随机在线问卷调查，调查结果分为四类：A.非常了解；B.了解较多；C.基本了解；D.了解较少.将收集到的信息进行了统计，绘制成不完整的统计表和统计图（如图所示）.请你根据统计图表所提供的信息解答下列问题.

频数分布统计表

类别	频数	频率
A	60	n
B	m	0.4
C	90	0.3
D	30	0.1

（1）接受问卷调查的学生共有人，m=，n=；
（2）补全条形统计图；
（3）学校决定从选填结果是A类的学生中，选取甲、乙、丙、丁四人，从这四位学生中随机抽取两名学生参与冬奥知识竞赛，用画树状图或列表的方法，求甲、乙两名同学同时被抽中的概率.

答案解析收藏纠错 + 选题

21. (2022九下·长沙月考) 如图，矩形ABCD的对角线AC，BD相交于点O，且DE∥AC，CE∥BD.
1. （1）求证：四边形OCED是菱形；
2. （2）若AB=3，AD=4，求四边形OCED的周长和面积.
答案解析收藏纠错 + 选题
22. (2022九下·长沙月考) 疫情期间，某口罩公司销售一种成本为每盒60元的口罩，规定试销期间销售单价不低于成本价，且获利不得高于30%，经试销发现，销售量y（万盒）与销售单价x（元）之同的函数图象如图.
1. （1）求y与x的函数关系式，并写出自变量x的取值范围：
2. （2）求当销售单价为多少时，销售利润最大，最大利润为多少万元？
答案解析收藏纠错 + 选题
23. (2022九下·长沙月考) 如图⊙O是△ABC的外接圆，AC是⊙O的直径，过圆心O的直线PF⊥AB于D，交⊙O于E，F，PB是⊙O的切线，B为切点，连接AP，AF.
1. （1）求证：直线PA为⊙O的切线；
2. （2）求证：AC²=4OD·OP；
3. （3）若BC=6， $\text{[math]}$ ，求AC的长.
答案解析收藏纠错 + 选题
24. (2022九下·长沙月考) 在平面直角坐标系中，我们不妨把纵坐标的值与横坐标的值的平方相等的点称为“雅心点”，例如点（ $\text{[math]}$ ， 1），（0，0），（ $\text{[math]}$ ， 2），…都是“雅心点”，显然，这样的“雅心点”有无数个.
1. （1）求一次函数 $\text{[math]}$ 上的所有“雅心点”的坐标为；
2. （2）若过点（1， $\text{[math]}$ ）的直线上恰好只有一个“雅心点”，请求出符合要求的直线解析式；
3. （3）若二次函数 $\text{[math]}$ （a是常数，a＞0）的图象上存在两个不同的“雅心点”，且“雅心点”的横坐标的值都不大于2，试求实数a的取值范围.
答案解析收藏纠错 + 选题
25. (2022九下·长沙月考) 如图，在矩形ABCD中，点E为边CD上的一点（且ED≤CE，且E点不与C、D重合），四边形ABCE关于直线AE的对称图形为四边形ANME，延长ME交AB于点P，连接BE，若AD=1.
1. （1）证明：AP=PE；
2. （2）若DE= $\text{[math]}$ ，求PE的值；
3. （3）延长BE交直线AN于点G，当∠AEB=90°时，记DE=x，四边形APEG的面积为S，求S与x的函数关系式.
答案解析收藏纠错 + 选题