一、选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
A . 1个
B . 2个
C . 3个
D . 4个
-
-
3.
(2021八上·无棣期中)
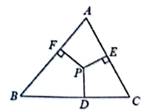
如图,点P是△ABC内一点,PD⊥BC,PE⊥AC,PF⊥AB,且PD=PE=PF,则点P是△ABC( )
A . 三边垂直平分线的交点
B . 三条角平分线的交点
C . 三条高所在直线的交点
D . 三条中线的交点
-
4.
(2021八上·无棣期中)
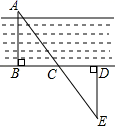
如图,要测量河两岸相对的两点A、B间的距离,先在垂直于

的河岸上作出线段

,并在

延长线上取一点D,使

,再过点D作垂线段

,使点E,C,A在一条直线上,则可判断

的理由是


-
A . 45°
B . 60°
C . 72°
D . 108°
-
-
A . 50°
B . 80°
C . 65°或50°
D . 50°或80°
-
8.
(2021八上·无棣期中)
如图,在△ABC中,∠B=40°,∠C=70°,AD是高,AE是角平分线,则∠DAE的度数为( )

A . 10°
B . 15°
C . 20°
D . 25°
-
9.
(2022八下·茂名期中)
如图,△ABC中,BC=14,边AB的垂直平分线和边AC的垂直平分线相交于点M,且与边BC分别相交于点D、E,连接AE、AD,则△AED的周长( )
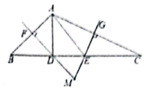
A . 14
B . 10
C . 18
D . 不能确定
-
10.
(2021八上·无棣期中)
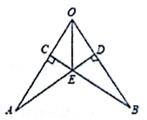
在测量一个小口圆形容器的壁厚时,小明用“X型转动钳"按如图方法进行测量,其中OA≈OD,OB=OC,测得AB=5厘米,即F=6厘米,圆形容器的壁厚是( )
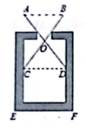
A . 5
B . 6
C . 2
D . 
-
11.
(2021八上·无棣期中)
如图,长方形纸片ABC)沿对角线折叠,设重叠部分为△EBD,那么下列说法
正确的有( )
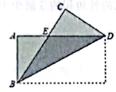
①△EBD是等腰三角形,EB=ED;
②折叠后∠ABE和∠CBD一定相等;
③折叠后得到的图形是轴对称图形
④△EBA和△EDC一定是全等三角形,
A . ①③④
B . ①②④
C . ①②③
D . ①②③④
-
12.
(2021八上·无棣期中)
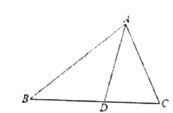
已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其正确的个数有( )个
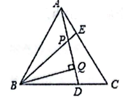
A . 1
B . 2
C . 3
D . 4
二、填空题(本大题共6个小题,每小题4分,共24分)
-
-
-
15.
(2021八上·无棣期中)
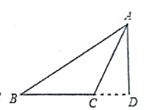
若△ABC中,∠ACB是钝角,AD⊥BC,垂足为D,若AD=6,BD=8,CD=3,则△ABC的面积等于
-
16.
(2021八上·无棣期中)
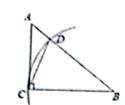
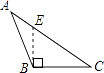
如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是
-
17.
(2021八上·无棣期中)
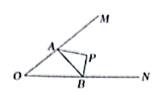
如图,∠MON=40°,点P是∠MON中的一个定点,点A、B分别在射线OM、ON移动,当△PAB的周长最小时,则∠APB的度数为
-
18.
(2021八上·无棣期中)
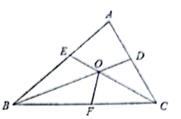
在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于F,则下列说法中正确的是
(填序号)①∠BOE=60°,②OE=OD,∠ABD=∠ACE,④BC=DE+CD.
三、解答题(本大题共6小题,共60分,解答时应写出必要的文字说明、证明过程或演算步骤)
-
-
-
21.
(2021八上·无棣期中)
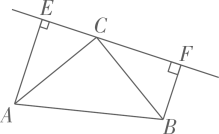
如图,在△ABC中,AC=BC,直线l经过点C,过A、B两点分别作直线l的垂线AE、BF,垂足分别为E、F,AE=CF,求证:∠ACB=90°
-
22.
(2021八上·无棣期中)
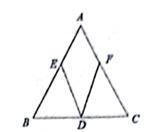
如图,△ABC中,AB=AC,D是DC的中点,B,P分别是AB、AC上的点,且AE=AF.求证:∠AED=∠APD
-
-
-
25.
(2021八上·无棣期中)
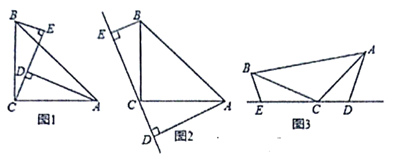
在学习完第12章后,刘老师让同学们独立完成课本56页第9题:“如图1,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm,求BE的长,”
-
-
(2)
待同学们完成这道题后,刘老师又出示了一道题:在课本原题其它条件不变的前提下,将CE所在直线旋转到△ABC的外部(如图2),请你猜想AD,DE,BE三者之间的数量关系,直接写出结论,不需证明.
-
(3)
如图3,将(1)中的条件改为:在△ABC中,AC=BC,D,C,E三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=α,其中α为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由。



 B .
B .  C .
C .  D .
D .