安徽省黄山市休宁县2021-2022学年九年级上学期第二次月...

更新时间：2022-01-20 浏览次数：77 类型：月考试卷

一、单选题

1. (2021九上·休宁月考) 抛物线 $\text{[math]}$ 的顶点坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021九上·休宁月考) 已知 $\text{[math]}$ 是方程x²﹣3 $\text{[math]}$ x+c＝0的一个根，则c的值是（）

A . ﹣6 B . 6 C . $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·休宁月考) 为了解学生假期每天帮忙家长做家务活动情况，学校团委随机抽取了部分学生进行线上调查，并将调查结果绘制成频数直方图（不完整，每组含最小值，不含最大值），并且知道80～100分钟占所抽查学生的17.5%，根据提供信息，以下说法错误的是（）

A . 本次共随机抽取了40名学生； B . 抽取学生中每天做家务时间的中位数落在40～60分钟这一组； C . 如果全校有800名学生，那么每天做家务时间超过1小时的大约有300人； D . 扇形统计图中0～20分钟这一组的扇形圆心角的度数是30°；

答案解析收藏纠错 + 选题
4. (2021九上·休宁月考) 抛物线y＝2x²与y＝－2x²相同的性质是（）

A . 开口向下 B . 对称轴是y轴 C . 有最低点 D . 对称轴是x轴

答案解析收藏纠错 + 选题
5. (2022九上·乐平期中) 某校高一年级今年计划招四个班的新生，并采取随机摇号的方法分班，小明和小红既是该校的高一新生，又是好朋友，那么小明和小红分在同一个班的机会是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·休宁月考) 如图，在⊙O中，弦AC∥半径OB，∠BOC＝48°，则∠OAB的度数为（）

A . 24° B . 30° C . 50° D . 60°

答案解析收藏纠错 + 选题
7. (2021九上·休宁月考) $\text{[math]}$ 是 $\text{[math]}$ 绕点O顺时针方向旋转 $\text{[math]}$ 后所得的图形，点C恰好在 $\text{[math]}$ 上，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·休宁月考) 若二次函数 $\text{[math]}$ 的对称轴是x=4，则关于x的方程 $\text{[math]}$ 的解为（　　）

A . x₁=0，x₂=8 B . x₁=1，x₂=9 C . x₁=1，x₂=﹣9 D . x₁=﹣1，x₂=9

答案解析收藏纠错 + 选题
9. (2023九上·新民期中) 已知等腰三角形的两边长分别是一元二次方程 $\text{[math]}$ 的两根，则该等腰三角形的底边长为（）

A . 2 B . 4 C . 8 D . 2或4

答案解析收藏纠错 + 选题
10. (2021九上·休宁月考) 如图，二次函数y＝ax²+bx+c的图象与y轴正半轴相交，其顶点坐标为（ $\text{[math]}$ ， 1），下列结论：①abc＜0；②b²﹣4ac＞0；③a+b＜0；④2a+c＜0，其中正确的个数是（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·罗平期中) 点（1，2）关于原点的对称点的坐标为．

答案解析收藏纠错 + 选题
12. (2021九上·休宁月考) 如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则BH的长度为．

答案解析收藏纠错 + 选题
13. (2021九上·休宁月考) 若一个圆锥的母线长为4，底面半径是1，则它的侧面展开图的面积是．

答案解析收藏纠错 + 选题
14. (2021九上·休宁月考) 我国魏晋时期的数学家刘徽首创“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的周长，进而确定圆周率．某圆的半径为R，其内接正十二边形的周长为C．若R＝ $\text{[math]}$ ，则C＝， $\text{[math]}$ ≈（结果精确到0.01，参考数据： $\text{[math]}$ ≈2.449， $\text{[math]}$ ≈1.414）．

答案解析收藏纠错 + 选题

三、解答题

15. (2022八下·昌平期末) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2021九上·休宁月考) 某汽车专卖店经销某种型号的汽车．已知该型号汽车的进价为15万元/辆，经销一段时间后发现：当该型号汽车售价定为25万元/辆时，平均每周售出8辆；售价每降低0.5万元，平均每周多售出1辆．
1. （1）当售价为22万元/辆时，求平均每周的销售利润．
2. （2）若该店计划平均每周的销售利润是90万元，为了尽快减少库存，求每辆汽车的售价．
答案解析收藏纠错 + 选题
17. (2021九上·休宁月考) 如图，在平面直角坐标系中，ΔABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，5）．

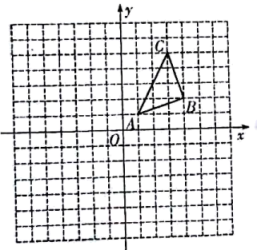
（1）请画出△ABC关于x轴的对称图形ΔA₁B₁C₁；
（2）借助网格，利用无刻度直尺画出线段CD，使CD平分ΔABC的面积．（保留确定点D的痕迹）．

答案解析收藏纠错 + 选题
18. (2021九上·休宁月考) 如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．
1. （1）求证：直线CD为⊙O的切线；
2. （2）当AB＝2BE，且CE＝ $\text{[math]}$ 时，求AD的长．
答案解析收藏纠错 + 选题
19. (2021九上·休宁月考) 小明同学在探究如何计算连续正整数之和后，得到公式S（n）＝1＋2＋3＋…＋n＝ $\text{[math]}$ ，于是他猜想连续正整数的平方和S（n²）是否也有类似的公式，为此，他将相关数值列成如下表格，请观察表格规律，并完成问题：
n
1
2
3
4
5
6
…
S（n）
1
3
6
10
15
a
…
S（n²）
1
5
14
b
55
91
…
$\text{[math]}$
1
$\text{[math]}$
$\text{[math]}$
c
$\text{[math]}$
d
…
1. （1）根据规律，表格中a＝；c＝；
2. （2）用含n的代数式表示 $\text{[math]}$ ；
3. （3）推导出计算公式S（n²）．
答案解析收藏纠错 + 选题
20. (2021九上·休宁月考) 转转盘和摸球是等可能概率下的经典模型．
1. （1）在一个不透明的口袋中，放入除颜色外其余都相同的4个小球，其中1个白球，3个黑球搅匀后，随机同时摸出2个球，求摸出两个都是黑球的概率(要求采用树状图或列表法求解)；
2. （2）如图，转盘的白色扇形和黑色扇形的圆心角分别为120°和240°．让转盘自由转动2次，求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解)．
答案解析收藏纠错 + 选题
21. (2021九上·新乡期末) 小红经营的网店以销售文具为主，其中一款笔记本进价为10元/本，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量y（单位：本）与线下售价x（单位：元/本， $\text{[math]}$ ，且x为整数）满足一次函数的关系，部分数据如下表：

x（元/本）

12

13

14

15

16

y（本）

120

110

100

90

80
1. （1）求y与x的函数关系式；
2. （2）若线上售价始终比线下每本便宜1元，且线上的月销量固定为40件．试问：当x为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．
答案解析收藏纠错 + 选题
22. (2021九上·休宁月考) 如图1，在△ABC中，AB＝AC，∠BAC＝α，点D、E分别在边AB、AC上，AD＝AE，连接DC，点F、P、G分别为DE、DC、BC的中点．
1. （1）观察猜想：图1中，线段PF与PG的数量关系是，∠FPG＝（用含α的代数式表示）
2. （2）探究证明：当△ADE绕点A旋转到如图2所示的位置时，小新猜想（1）中的结论仍然成立，请你证明小新的猜想．
答案解析收藏纠错 + 选题
23. (2021九上·休宁月考) 如图，抛物线y=ax² + bx + c 交x轴于A、B两点，交y轴于点C，对称轴为直线x=1，已知：A(-1，0)、C(0，-3)．
1. （1）求抛物线y= ax² + bx + c 的解析式；
2. （2）求△AOC和△BOC的面积比；
3. （3）在对称轴上是否存在一个P点，使△PAC的周长最小．若存在，请你求出点P的坐标；若不存在，请你说明理由．
答案解析收藏纠错 + 选题