题库组卷系统-专注K12在线组卷服务

在线咨询

当前：高中数学

当前位置：高中数学 /高考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

上海市奉贤区2022届高三数学一模试卷

更新时间：2022-07-05 浏览次数：87 类型：高考模拟

一、填空题

1. (2022·奉贤模拟) 已知集合 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
2. (2022·奉贤模拟) 计算 $\text{[math]}$ .

答案解析收藏纠错 + 选题
3. (2022·奉贤模拟) 已知圆的参数方程为 $\text{[math]}$ （ $\text{[math]}$ 为参数），则此圆的半径是.

答案解析收藏纠错 + 选题
4. (2022·奉贤模拟) 函数 $\text{[math]}$ 的最小正周期是.

答案解析收藏纠错 + 选题
5. (2022·奉贤模拟) 函数 $\text{[math]}$ 是奇函数，则实数 $\text{[math]}$ .

答案解析收藏纠错 + 选题
6. (2022·奉贤模拟) 若圆锥的底面面积为 $\text{[math]}$ ，母线长为2，则该圆锥的体积为.

答案解析收藏纠错 + 选题
7. (2022·奉贤模拟) 函数 $\text{[math]}$ 的定义域是.

答案解析收藏纠错 + 选题
8. (2022·奉贤模拟) 等差数列 $\text{[math]}$ 满足 $\text{[math]}$ ，则数列 $\text{[math]}$ 前 $\text{[math]}$ 项的和为.

答案解析收藏纠错 + 选题
9. (2022·奉贤模拟) 汽车前灯反射镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反射镜的轴垂直，灯泡位于抛物线焦点处，已知灯口的直径是24 cm，灯深10 cm，那么灯泡与反射镜顶点(即截得抛物线顶点)间的距离是.

答案解析收藏纠错 + 选题
10. (2022·奉贤模拟) 已知曲线 $\text{[math]}$ 的焦距是10，曲线上的点 $\text{[math]}$ 到一个焦点的距离是2，则点 $\text{[math]}$ 到另一个焦点的距离为.

答案解析收藏纠错 + 选题
11. (2022·奉贤模拟) 从集合 $\text{[math]}$ 中任取3个不同元素分别作为直线方程 $\text{[math]}$ 中的 $\text{[math]}$ ，则经过坐标原点的不同直线有条（用数值表示）

答案解析收藏纠错 + 选题
12. (2022·奉贤模拟) 设平面上的向量 $\text{[math]}$ 满足关系 $\text{[math]}$ ，又设 $\text{[math]}$ 与 $\text{[math]}$ 的模均为1且互相垂直，则 $\text{[math]}$ 与 $\text{[math]}$ 的夹角取值范围为.

答案解析收藏纠错 + 选题

二、单选题

13. (2022·奉贤模拟) 下列函数中为奇函数且在 $\text{[math]}$ 上为增函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2022·奉贤模拟) 已知 $\text{[math]}$ 的二项展开式中，前三项系数成等差数列，则 $\text{[math]}$ 的值为（）

A . 7 B . 8 C . 9 D . 10

答案解析收藏纠错 + 选题
15. (2022·奉贤模拟) 对于下列命题：
①若 $\text{[math]}$ 则 $\text{[math]}$ ；
②若 $\text{[math]}$ ，则 $\text{[math]}$ .
关于上述命题描述正确的是（）

A . ①和②均为真命题 B . ①和②均为假命题 C . ①为真命题，②为假命题 D . ①为假命题，②为真命题

答案解析收藏纠错 + 选题
16. (2022·奉贤模拟) 复数 $\text{[math]}$ 的模为1，其中 $\text{[math]}$ 为虚数单位， $\text{[math]}$ ，则这样的 $\text{[math]}$ 一共有（）个.

A . 9 B . 10 C . 11 D . 无数

答案解析收藏纠错 + 选题

三、解答题

17. (2022·奉贤模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ 所对边 $\text{[math]}$ 满足 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的值；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的周长.
答案解析收藏纠错 + 选题
18. (2022·奉贤模拟) 第一象限内的点 $\text{[math]}$ 在双曲线 $\text{[math]}$ 上，双曲线的左､右焦点分别记为 $\text{[math]}$ ，已知 $\text{[math]}$ 为坐标原点.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 的面积为2，求点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
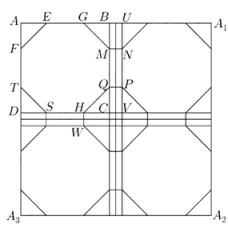
19. (2022·奉贤模拟) 图1是某会展中心航拍平面图，由展览场馆､通道等组成，可以假设抽象成图2，图2中的大正方形 $\text{[math]}$ 是由四个相等的小正方形（如 $\text{[math]}$ ）和宽度相等的矩形通道组成.展览馆可以根据实际需要进行重新布局成展览区域和休闲区域，展览区域由四部分组成，每部分是八边形，且它们互相全等.图2中的八边形EFTSHQMG是小正方形 $\text{[math]}$ 中的展览区域，小正方形 $\text{[math]}$ 中的四个全等的直角三角形是休闲区域，四个八边形是整个的展览区域，16个全等的直角三角形是整个的休闲区域.设 $\text{[math]}$ 的边长为300米， $\text{[math]}$ 的周长为180米.
1. （1）设 $\text{[math]}$ ，求 $\text{[math]}$ 的面积 $\text{[math]}$ 关于 $\text{[math]}$ 的函数关系式；
2. （2）问 $\text{[math]}$ 取多少时，使得整个的休闲区域面积最大.( $\text{[math]}$ ，长度精确到1米，利用精确后的长度计算面积，面积精确到1平方米)
答案解析收藏纠错 + 选题
20. (2022高一下·中山期末) 如图，在正四棱锥 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ 的中点，平面 $\text{[math]}$ 与棱 $\text{[math]}$ 的交点为 $\text{[math]}$ .
1. （1）求异面直线 $\text{[math]}$ 与 $\text{[math]}$ 所成角的大小；
2. （2）求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 所成锐二面角的大小；
3. （3）求点 $\text{[math]}$ 的位置.
答案解析收藏纠错 + 选题
21. (2022·奉贤模拟) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，求证：数列 $\text{[math]}$ 不可能是常数列；
2. （2）若 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项的和；
3. （3）当 $\text{[math]}$ 时，令 $\text{[math]}$ ，判断对任意 $\text{[math]}$ ， $\text{[math]}$ 是否为正整数，请说明理由.
答案解析收藏纠错 + 选题

试卷信息