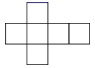
 B .
B . 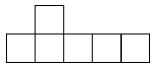 C .
C . 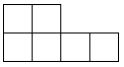 D .
D . 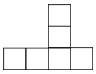


|
项目 选手 |
主题契合度 |
语言表达能力 |
诗歌感染力 |
综合印象 |
|
李华 |
90 |
80 |
88 |
90 |
|
张丽 |
90 |
85 |
85 |
95 |
根据以上信息,解答下列问题:
(问题提出)
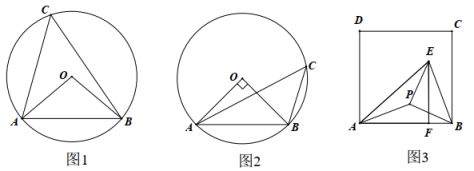
如图1,为
的一条弦,点
在弦
所对的优弧上运动时,根据圆周角性质,我们知道
的度数不变.爱动脑筋的小芳猜想,如果平面内线段
的长度已知,
的大小确定,那么点
是不是在某个确定的圆上运动呢?
(问题探究)
为了解决这个问题,小芳先从一个特殊的例子开始研究.如图2,若 , 线段
上方一点
满足
, 为了画出点
所在的圆,小芳以
为底边构造了一个
, 再以点
为圆心,
为半径画圆,则点
在
上.后来小芳通过逆向思维及合情推理,得出一个一般性的结论.即:若线段
的长度已知,
的大小确定,则点
一定在某一个确定的圆上,即定弦定角必定圆,我们把这样的几何模型称之为“定弦定角”模型.
(模型应用)
①求的度数;
②连接 , 若正方形
的边长为
, 求
的最小值.