 B .
B .  C .
C .  D .
D . 


 B .
B .  C .
C .  D .
D . 
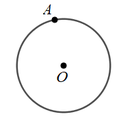
已知:点A在上.
求作:直线PA和相切.
作法:如图,
①连接AO;
②以A为圆心,AO长为半径作弧,与的一个交点为B;
③连接BO;
④以B为圆心,BO长为半径作圆;
⑤作的直径OP;
⑥作直线PA.
所以直线PA就是所求作的的切线.
根据小亮设计的尺规作图过程,
证明:在中,连接BA.
∵ ,
,
∴ .
∴点A在上.
∵OP是的直径,
∴( ▲ )(填推理的依据).
∴ .
又∵点A在上,
∴PA是的切线( ▲ )(填推理的依据).

x | 0 | 1 | 2 | 3 | 4 | … | ||||
y | 0 | 2 | 1 | 0 | 2 | … |
结合上表,画出当时,函数
的图象;
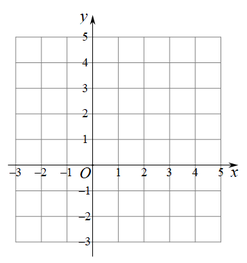
若关于x的方程有一个实数根为2,则该方程其它的实数根约为(结果保留小数点后一位).

已知点 ,
,
,
.