2021年吉林省长春市双阳区中考数学二模试题

更新时间：2022-04-18 浏览次数：108 类型：中考模拟

一、单选题

1. (2021·双阳模拟) 实数a，b在数轴上对应的点的位置如图所示，下列结论正确的是（）

A . a＞b B . ﹣a＜b C . a＞﹣b D . ﹣a＞b

答案解析收藏纠错 + 选题
2. (2022·成都模拟) 下列运算中，正确的是（）

A . 2a³﹣a³＝2 B . （a³）²＝a⁹ C . 2a²•3a³＝6a⁶ D . a⁷÷a⁵＝a²

答案解析收藏纠错 + 选题
3. (2021·双阳模拟) 下面简单几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·双阳模拟) 判断一元二次方程x²﹣2x﹣2＝0的根的情况是（）

A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 没有实数根 D . 只有一个实数根

答案解析收藏纠错 + 选题
5. (2022·易县模拟) 如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE＝30cm，EF＝15cm，测得边DF离地面的高度AC＝1.6m，CD＝10m，则树高AB长为（）

A . 21.6m B . 6.6m C . 20.6m D . 7.6m

答案解析收藏纠错 + 选题
6. (2021·双阳模拟) 如图，在平面直角坐标系中，两条直线分别为y＝2x，y＝kx，且点A在直线y＝2x上，点B在直线y＝kx上，AB∥x轴，AD⊥x轴，BC⊥x轴垂足分别为D和C，若四边形ABCD为正方形时，则k＝（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
7. (2021·双阳模拟) 如图，在△ABC中，∠ACB＝90°，AB＝10，以点A为圆心，适当长为半径作弧，交AB于点D，交AC于点E，再以E为圆心，等于DE长为半径作弧，两弧交于点F，在射线AF上取点G，H为BG的中点，连接CH，若AG＝6，则CH长为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2021·双阳模拟) 如图，在平面直角坐标系中，抛物线y＝﹣x²+4x+m的顶点为A，它与x轴分别交于B，C两点，与y轴的交点为D，过点D作DE平行于x轴交于抛物线于点E，BF∥CE交DE于点F，若3S_△ABC＝4S_△FEC ，则m的值为（）

A . ﹣ $\text{[math]}$ B . ﹣ $\text{[math]}$ C . ﹣12 D . 12

答案解析收藏纠错 + 选题

二、填空题

9. (2021·双阳模拟) 计算 $\text{[math]}$ =。

答案解析收藏纠错 + 选题
10. (2021·双阳模拟) 不等式组 $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题
11. (2021·双阳模拟) 如图，直线a∥b，直线l与a，b分别交于点A，B，过点A作AC⊥b于点C，若∠1＝50°，则∠2的度数为．

答案解析收藏纠错 + 选题
12. (2021·双阳模拟) 如图，矩形纸片ABCD中，AB＝6，BC＝10，先按图②操作：将矩形纸片ABCD沿过点A的直线折叠，使点B落在边AD上的点E处，折痕为AF；再按图③操作，沿过点E的直线折叠，使点D落在EF上的点H处，折痕为EG，则FH＝．

答案解析收藏纠错 + 选题
13. (2021·双阳模拟) 如图，在A处看建筑物CD的顶端C的仰角为α，且tanα＝0.8，向前行进3米到达B处，从B处看顶端C的仰角为45°（图中各点均在同一平面内，A、B、D三点在同一条直线上，CD⊥AD，则建筑物CD的高度为米．

答案解析收藏纠错 + 选题
14. (2021·双阳模拟) 在平面直角坐标系中，OA＝AB，∠OAB＝90°，反比例函数y＝ $\text{[math]}$ （x＞0）的图象经过A和B两点其中A（n，1），且点B的纵坐标为n，则n＝．

答案解析收藏纠错 + 选题

三、解答题

15. (2021·双阳模拟) 先化简，再求值： $\text{[math]}$ ，其中a＝ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2021·双阳模拟) 《孙子算经》是中国古代重要的数学著作，其中有一段文字的大意是：甲、乙两人各有若干钱，如果甲得到乙所有钱的一半，那么甲共有钱48文；如果乙得到甲所有钱的 $\text{[math]}$ ，那么乙也共有钱48文.甲、乙两人原来各有多少钱？

答案解析收藏纠错 + 选题
17. (2023·靖宇模拟) 为弘扬中华优秀传统文化，某校开展“经典诵读”比赛活动，诵读材料有《论语》、《大学》、《中庸》（依次用字母 $\text{[math]}$ 表示这三个材料），将 $\text{[math]}$ 分别写在3张完全相同的不透明卡片的正面上，背面朝上洗匀后放在桌面上，比赛时小勇先从中随机抽取一张卡片，记下内容后放回，洗匀后，再由小智从中随机抽取一张卡片，他俩按各自抽取的内容进行诵读比赛．请用列表或面树状图的方法求他俩诵读两个不同材料的概率．

答案解析收藏纠错 + 选题
18. (2021·双阳模拟) 某校500名学生参加植树活动，要求每人植5～8棵，活动结束后随机抽查了30名学生每人的植树量，并分为四种类型，A：5棵；B：6棵；C：7棵；D：8棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处不符合题意．

回答下列问题：
1. （1）写出条形图中存在的错误，并说明理由．
2. （2）在扇形统计图中，A所在的扇形的圆心角为度．
3. （3）写出这30名学生每人植树量的众数，中位数．
4. （4）求这30名学生每人植树量的平均数，并估计这500名学生共植树多少棵．
答案解析收藏纠错 + 选题
19. (2021·双阳模拟) 如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线．交BC于点E．
1. （1）求证：BE＝EC．
2. （2）填空：若∠B＝30°，DE＝ $\text{[math]}$ ，则弧DC的长度为．
  注：第（2）小题直接写出结果．
答案解析收藏纠错 + 选题
20. (2021·双阳模拟) 在6×6的正方形网格中，△ABC的顶点均在格点上，请用无刻度直尺画图．（保留必要的画图痕迹）
1. （1）在图1中，画一个与∠BAC相等的∠BDC，且点D在格点上．
2. （2）在图2中，画一个与△ABC面积相等，且以BC为边的平行四边形BCDE，D、E均在格点上．
3. （3）在图3中，在AC上找一点D，连接BD，使△ABD的面积是△BCD面积的4倍．
答案解析收藏纠错 + 选题
21. (2021·双阳模拟) 一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶．设行驶的时间为x（时），两车之间的距离为y（千米），图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系．
1. （1）根据图中信息，求线段AB所在直线的函数解析式和甲乙两地之间的距离．
2. （2）已知两车相遇时快车比慢车多行驶20千米，若快车从甲地到达乙地所需时间为t时，求t的值．
3. （3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象．
答案解析收藏纠错 + 选题
22. (2021·双阳模拟) 【教材呈现】下图是华师版九年级上册数学教材102﹣103页的部分内容．
性质：直角三角形的斜边中线等于斜边的一半给出上述性质证明中的部分演绎推理的过程如下：已知：如图1，在△ABC中，∠ACB＝90°，CD为斜边AB上的中线．求证：CD＝AB.证明：如图2，延长CD至点E，使DE＝CD，连接AE，BE．
1. （1）【问题解决】请结合图3将证明过程补充完整．
2. （2）【应用探究】
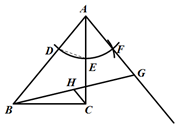
  如图4，在△ABC中，AD是高，CE是中线，点F是CE的中点，DF⊥CE，点F为垂足，∠AEC＝78°，则∠BCE为度．
3. （3）如图5，在线段AC上有一点B，AB＝4，AC＝11，分别以AB和BC为边作正方形ABED和正方形BCFG，点E落在边BG上，连接DF，点H为DF的中点，连接GH，则GH的长为．
答案解析收藏纠错 + 选题
23. (2021·双阳模拟) 如图，在平行四边形ABCD中，∠A＝60°，对角线BD⊥AD，AB＝8，点P从点C出发沿CD以每秒2个单位长度的速度向终点D运动，过点P作PE⊥DC交折线CB﹣BA于点E，以PE为边作等边三角形PEQ，点Q、B在PE的同侧，设点P的运动时间为t秒．
1. （1）求PE（用含t的代数式表示）．
2. （2）当点Q落在BC上时，求t的值．
3. （3）若△PQE与平行四边形ABCD重合部分图形的面积为S，求S与t之间的函数关系式．
4. （4）点P关于直线QC的对称点P'，当P'Q⊥AB时，直接写出t的值．
答案解析收藏纠错 + 选题
24. (2021·双阳模拟) 在平面直角坐标系中，函数y＝x²﹣4mx﹣3m（m为常数）的图象记作G．
1. （1）设图象G的顶点的坐标为（x₀ ， y₀），
  ①求y₀的值（用含x₀的代数式表示）．
  ②求证：y₀≤ $\text{[math]}$ ．
2. （2）将图象G平移后得到的图象记作W，且W过原点，W对应的函数关系式为y＝a（x﹣h）²+k，在x≤2的条件下，W对应的函数y的值随x的增大而减小，直接写出k的取值范围．
3. （3）设图象G在﹣2m≤x≤2m+1之间部分的图象为G₁ ，
  ①当G₁的最高点的纵坐标为4时，求m的值．
  ②若点A（﹣2m，﹣1），B（2m+1，﹣1），C（2m+1，1），D（﹣2m，1），直接写出矩形ABCD与y＝x²﹣4mx﹣3m有两个交点时m的取值范围．
答案解析收藏纠错 + 选题