浙江省金华市义乌市绣湖中学2021-2022学年九年级下学期...

更新时间：2024-07-31 浏览次数：109 类型：开学考试

一、选择题(本题有10小题,每小题3分,共30分)

1. (2022九下·义乌开学考) ﹣2的相反数是（）

A . ﹣2 B . 2 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九下·义乌开学考) 已知x²﹣4x﹣1＝0，则代数式x（x﹣4）+1的值为（）

A . 0 B . 1 C . 2 D . ﹣1

答案解析收藏纠错 + 选题
3. (2022九下·义乌开学考) 如图，D为平面直角坐标系内一点，OD与x轴构成∠1，那么tan∠1=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九下·义乌开学考) 关于反比例函数 $\text{[math]}$ 图象，下列说法正确的是（）

A . 必经过点（1，1） B . 两个分支分布在第二、四象限 C . 两个分支关于x轴成轴对称 D . 两个分支关于原点成中心对称

答案解析收藏纠错 + 选题
5. (2022九下·义乌开学考) 一组数据为1，5，3，4，5，6，这组数据的众数、中位数分别为（）

A . 4，5 B . 3，2 C . 5，4 D . 5，4.5

答案解析收藏纠错 + 选题
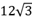
6. (2022九下·义乌开学考) 如图，在⊙O中，弦AB的长是 cm，弦AB的弦心距为6cm，E是⊙O优弧AEB上一点.则∠AEB的度数为（）

A . 60° B . 45° C . 30° D . 80°

答案解析收藏纠错 + 选题
7. (2022九下·义乌开学考) 如图，在△ABC中，∠ACB=90°，CD⊥AB，若AD=4，BD=8，则CD的长为（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九下·义乌开学考) 如图，某物流公司指示标AB边长是40cm，AB=AC，∠ABC=45°，则该指示标BC的宽的值应是（）

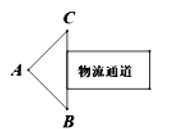
A . $\text{[math]}$ B . 40 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九下·义乌开学考) 如图，在平面直角坐标系中，半径为5的⊙E与y轴交于点A(0，-2)，B（0，4），与x轴交于C，D，则点D的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·珠海模拟) 如图，已知点A（ $\text{[math]}$ ，2）， B(0，1)，射线AB绕点A逆时针旋转30°，与x轴交于点C，则过A，B，C三点的二次函数y=ax²+bx+1中a，b的值分别为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题 (本题有6小题,每小题4分,共24分)

11. (2022九下·义乌开学考) 分解因式：a²﹣ab＝；

答案解析收藏纠错 + 选题
12. (2022九下·义乌开学考) 关于x的一元二次方程 $\text{[math]}$ +tanα=0有两个相等的实数根，则锐角α = ．

答案解析收藏纠错 + 选题
13. (2022九下·义乌开学考) ⊙O的半径为10，弦AB//CD，AB=12，CD=16，则AB与CD之间的距离为．

答案解析收藏纠错 + 选题
14. (2022九下·义乌开学考) 如图，甲、乙、丙3人站在5×6网格中的三个格子中，小王随机站在剩下的空格中，与图中3人均不在同一行或同一列的概率是．

答案解析收藏纠错 + 选题
15. (2022九下·义乌开学考) 当0≤x≤4时，直线y=2x+a与抛物线y=（x-1）²-3有2个不同交点，则a的取值范围是．

答案解析收藏纠错 + 选题
16. (2022九下·义乌开学考) 足球射门时，在不考虑其他因素的条件下，射点到球门AB的张角越大，射门越好. 当张角达到最大值时，我们称该射点为最佳射门点. 通过研究发现，如图1所示，一学生带球在直线CD上行进时，当存在一点Q，使得∠CQA=∠ABQ（此时也有∠DQB=∠QAB）时，恰好能使球门AB的张角∠AQB达到最大值，故可以称点Q为直线CD上的最佳射门点.如图2所示，是一个矩形形状的足球场，AB为球门一部分，CD⊥AB于点D，AB=6米，BD=2米.某球员沿CD向球门AB进攻，设最佳射门点为点Q.
1. （1） tan∠AQB= ．
2. （2）已知对方守门员伸开双臂后，成功防守的范围为 $\text{[math]}$ ，若此时守门员站在张角∠AQB内，双臂张开MN垂直于AQ进行防守，为了确保防守成功，MN中点与AB的距离至少为．
答案解析收藏纠错 + 选题

三、解答题（本题有8小题,共66分）

17. (2022九下·义乌开学考) 计算：|－4|－ $\text{[math]}$ －(－ $\text{[math]}$ )^－²+2cos 45°

答案解析收藏纠错 + 选题
18. (2022九下·义乌开学考) 已知5x²﹣x﹣1＝0，求代数式（3x+2）（3x﹣2）+x（x﹣2）的值．

答案解析收藏纠错 + 选题
19. (2022九下·义乌开学考) 如图1为医院里常见的“测温门”，图2为该“测温门”截面示意图．小聪做了如下实验：当他在地面M处时“测温门”开始显示额头温度，此时在额头B处测得A的仰角为30°；当他在地面N处时，“测温门”停止显示额头温度，此时在额头C处测得A的仰角为60°．经测量该测温门的高度AD为2.5米，小聪的有效测温区间MN的长度是1米，根据以上数据，求小聪的身高CN为多少？（注：额头到地面的距离以身高计）（参考数据： $\text{[math]}$ ，结果精确到0.01米）

答案解析收藏纠错 + 选题
20. (2022九下·义乌开学考) 如图，在正方形网格中，△ABC的顶点在格点上．请仅用无刻度直尺完成以下作图（保留作图痕迹）．
1. （1）在图1中，作△ABC关于点O对称的△A'B'C'；
2. （2）在图2中，作△ABC绕点A顺时针旋转一定角度后，顶点仍在格点上的△AB'C'．
答案解析收藏纠错 + 选题
21. (2022九下·义乌开学考) 如图，在矩形ABCD中，AB=5，BC=4，点E是AB上一点，CE=1，点F是线段AB上一个动点，以EF为斜边向上作等腰直角三角形.
1. （1）当BF=5时，求BG的长度．
2. （2）点F从点B运动到点A的过程中，求AG的最小值．
答案解析收藏纠错 + 选题
22. (2022九下·义乌开学考) 甲、乙两组同学玩“两人背夹球”比赛，即：每组两名同学用背部夹着球跑完
规定的距离，若途中球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲组两位同学掉了球；乙组两位同学则顺利跑完．设比赛距离用y表示，单位是米；比赛时间用x表示，单位是秒.两组同学比赛过程用图象表示如下.
1. （1）这是一次米的背夹球比赛，获胜的是组同学；
2. （2）请写出线段AB的实际意义；
3. （3）求出C点坐标并说明点C的实际意义.
答案解析收藏纠错 + 选题
23. (2022九下·义乌开学考) 如图1，已知点O在四边形ABCD的边AB上，且OA＝OB＝OC＝OD＝2，OC平分∠BOD，与BD交于点G，AC分别与BD、OD交于点E、F．
1. （1）求证：OC∥AD；
2. （2）如图2，若DE＝DF，求 $\text{[math]}$ 的值；
3. （3）当四边形ABCD的周长取最大值时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2022九下·义乌开学考) 如图，抛物线y=ax²+bx+c经过点A（-1，0）点B（3，0），点C（0，3），D为抛物线的顶点.
1. （1）求抛物线的表达式；
2. （2）连接AC，M是平面内一点，将△OAC绕点M沿逆时针旋转90^o后，得到△O₁A₁C₁ ，点O、A、C对应的点分别是点O₁、A₁、C₁ ，若△O₁A₁C₁的两个顶点恰好落在抛物线上，求出点C₁的横坐标；
3. （3）在坐标平面内找一点P，使△OCD与△CBP相似，且 ∠COD=∠BCP，求出所有点P的坐标．
答案解析收藏纠错 + 选题