
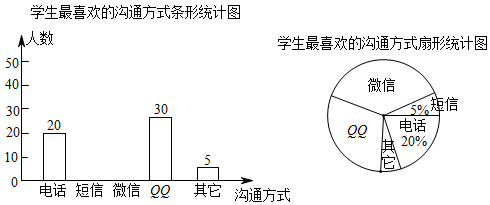



①求 与
的函数表达式;
②在前六周中,哪一周的销售额 (元)最大?最大销售额是多少?
下面,我们通过折叠的方式折出一个 矩形,如图a所示.
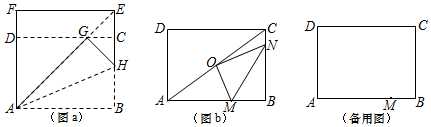
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为 矩形.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求 的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2 ,则DR的最小值= ▲ .