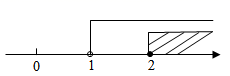
 B .
B .  C .
C . 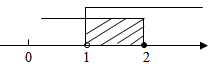 D .
D . 


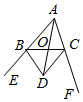
解不等式组: 解:去分母,得2(x+2)﹣6<3(2x﹣1)……第一步 去括号,得2x+4﹣6<6x﹣3.……第二步 移项,合并同类项,得﹣4x<﹣1.……第三步 两边同时除以﹣4,得x<﹣ |
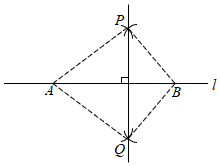
已知直线l和l外一点P,下面是小明设计的“过点P作直线的垂线”的作法:
请结合图形阅读作法,并将证明“PQ⊥l”的过程补充完整.
作法:①在直线上取点A,B;
②分别以点A、B为圆心,AP、BP为半径作弧,两弧在直线l下方交于点Q;
③作直线PQ.
结论:PQ⊥l,且PQ经过点P.
证明:连接AP,AQ,BP,BQ.
由作法可知,AP=AQ,BP=BQ.
∴点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,(依据 )
∴直线AB是线段PQ的垂直平分线(依据: )
∴PQ⊥l.

( 1 )图中线段AB的长度为 ;
( 2 )将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1 , 画出△A1B1C1;
( 3 )将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2 , 直接写出点A2、C2的坐标.