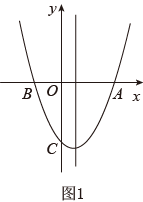
 B .
B .  C .
C .  D .
D . 
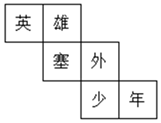
![]()
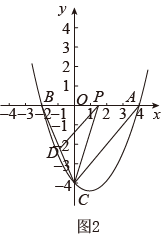
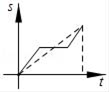 B .
B . 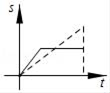 C .
C . 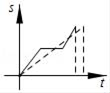 D .
D . 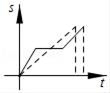

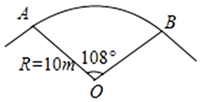

根据统计图提供的信息,解答下列问题:
若在甲地销售,每件售价y(元)与x之间的函数关系式为y=﹣x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).
若在乙地销售,受各种不确定因素的影响,每件成本为a元(a为常数,18≤a≤25),每件售价为98元,销售x(件)每年还需缴纳x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为a1 , 排在第二位的数称为第二项,记为a2 , 依此类推,排在第n位的数称为第n项,记为an , 所以,数列的一般形式可以写成:a1 , a2 , a3 , …,an , ….
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.
如:数列1,3,5,7,…为等差数列,其中a1=1,a2=3,公差为d=2.
根据以上材料,解答下列问题: