吉林省吉林市永吉县2020-2021学年七年级下学期期中考试...

更新时间：2022-03-24 浏览次数：54 类型：期中考试

一、单选题

1. (2024七下·云梦期末) 下列各图中，∠1和∠2是对顶角的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021七下·永吉期中) 如图所示，四幅汽车标志设计中，能通过平移得到的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021七下·永吉期中) 式子 $\text{[math]}$ 的值为（）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021七下·永吉期中) 在-3.14， $\text{[math]}$ ， 0， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， 0.1010010001…中，无理数的个数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2021七下·永吉期中) 如图，点E在BA的延长线上，点F在BD的延长线上．下列选项中能判定AB∥CD的是（）

A . ∠1＝∠2 B . ∠3＝∠4 C . ∠5＝∠B D . ∠6＝∠C

答案解析收藏纠错 + 选题

二、填空题

6. (2024九下·秦安模拟) $\text{[math]}$ 的相反数是．

答案解析收藏纠错 + 选题
7. (2021七下·永吉期中) 如图，AB与DE相交于点O，OC⊥AB，∠AOE＝55° ，则∠COD的度数是．

答案解析收藏纠错 + 选题
8. (2021七下·永吉期中) 在平面直角坐标系中，若点A（－3，a）在第二象限，则点B（5，－a）第象限．

答案解析收藏纠错 + 选题
9. (2021七下·永吉期中) 在平面直角坐标系中，点A（m，n）在第三象限，则m＋n的值可以是（写出满足条件的一个值即可）．

答案解析收藏纠错 + 选题
10. (2022七下·鞍山期中) 如图，某单位要在河岸 $\text{[math]}$ 上建一个水泵房引水到C处，他们的做法是：过点C作 $\text{[math]}$ 于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是．

答案解析收藏纠错 + 选题
11. (2021七下·永吉期中) 如图，若点A的坐标为（1，2），若点B的坐标为（-2，1），则点C的坐标为．

答案解析收藏纠错 + 选题
12. (2021七下·永吉期中) 若点A（m-1，m+2）在x轴上，则点A的坐标为．

答案解析收藏纠错 + 选题
13. (2021七下·永吉期中) 长方形OABC在平面直角坐标系中的位置如图所示，其中的三个顶点分别为O（0，0），A（5，0），C（0，3）．将长方形OABC沿x轴向右平移3个单位长度，得到长方形O₁A₁B₁C₁ ，则长方形O₁A₁B₁C₁与长方形OABC重合部分的周长为．

答案解析收藏纠错 + 选题

三、解答题

14. (2021七下·永吉期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023七下·泾阳期中) 如图，O为直线AB上一点，OC⊥AB，并且∠AOD＝130°．求∠COD的度数．

答案解析收藏纠错 + 选题
16. (2021七下·永吉期中) 在平面直角坐标系中，已知O，A，B，C四点的坐标分别为O（0，0），A（0，3），B（－3，3），C（－3，0）．
1. （1）在平面直角坐标系中，描出O，A，B，C四点；
2. （2）依次连接OA，AB，BC，CO后，得到图形的形状是．
答案解析收藏纠错 + 选题
17. (2021七下·永吉期中) 如图，直线a和直线b被直线c，d所截，若∠1＝70°，∠2＝70°，∠3＝80°．求∠4的度数．

答案解析收藏纠错 + 选题
18. (2021七下·永吉期中) 如图所示，点P是∠AOB的OA边上一点．
1. （1）过点P作CD∥OB（C，D两点分别在OA的左、右两侧），作PE⊥OB，垂足为E；
2. （2）若∠O＝65°，则∠OPE的度数是，∠OPC的度数是，∠APE的度数是．
答案解析收藏纠错 + 选题
19. (2021七下·永吉期中) 若8的立方根是a，b的算术平方根是3，m的两个平方根分别是5和n．
1. （1）求 $\text{[math]}$ 的平方根；
2. （2）求 $\text{[math]}$ 的立方根．
答案解析收藏纠错 + 选题
20. (2021七下·永吉期中) 如图，DG∥AB，∠1＝∠2，EF⊥AC于F，判断BD与AC的位置关系，并说明理由．

答案解析收藏纠错 + 选题
21. (2021七下·永吉期中) 如图，E为DF上的一点，B为AC上一点，如果∠1＝∠2，∠C＝∠D．
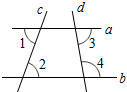
求证：DF∥AC．
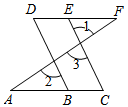
以下是小明同学的证明过程，请你帮他完成填空：
证明：∵∠1＝∠2（已知），
又∵∠1＝∠3（                  ▲                  ），
∴∠2＝                  ▲                  （等量代换）．
∴                  ▲                  ∥                  ▲                  （                  ▲                  ）．
∴∠C＝∠ABD （                  ▲                  ）．
∵∠C＝∠D（已知），
∴∠D＝∠ABD（等量代换）．
∴DF∥AC（                  ▲                  ）．

答案解析收藏纠错 + 选题
22. (2021七下·永吉期中) 已知，如图，BC与DE相交于点O，给出下面三个论断：①∠B＝∠E；②AB∥DE；③BC∥EF．请以其中的两个论断为条件，填入“题设”栏中；剩下的论断为结论，填入“结论”栏中，使之成为一个真命题，并加以证明．
题设：已知：如图，BC与DE相交于点O， ▲ ， ▲ （填序号）．
结论： ▲ （填序号）．
证明：

答案解析收藏纠错 + 选题
23. (2021七下·永吉期中) 根据下表回答下列问题：
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
17
x²
256
159.21
262.44
265.69
268.96
272.25
275.56
278.89
282.24
285.62
289
1. （1） 289的算术平方根是， $\text{[math]}$ ＝；
2. （2） $\text{[math]}$ ＝，275.56的平方根是；
3. （3） $\text{[math]}$ ＝， $\text{[math]}$ ＝；
4. （4）若 $\text{[math]}$ （x＞0），则 $\text{[math]}$ ＝（用含a的式子表示）．
答案解析收藏纠错 + 选题
24. (2021七下·永吉期中) 在平面直角坐标系中，点A的坐标为（2，a），点B的坐标为（b，－4），点C的坐标为（c，0），并且a，b，c满足 $\text{[math]}$ ．
1. （1） a＝，b＝，c＝，在平面直角坐标系中，画出△ABC；
2. （2）求△ABC的面积S；
3. （3）把△ABC向上平移2个单位长度，再向左平移4个单位长度，得到△A₁B₁C₁ ，直接画出平移后的△A₁B₁C₁（点A的对应点是A₁ ，点B的对应点是B₁ ，点C的对应点是C₁），点B₁的坐标为．
答案解析收藏纠错 + 选题
25. (2021七下·永吉期中) 阅读下面文字：
我们知道： $\text{[math]}$ 是无理数，而无理数是无限不循环小数，因此 $\text{[math]}$ 的小数部分我们不可能全部写出来，于是小明用 $\text{[math]}$ 来表示 $\text{[math]}$ 的小数部分，事实上小明的表示法是有道理的，因为 $\text{[math]}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：由“平方与开平方互为逆运算”可知： $\text{[math]}$ ＜ $\text{[math]}$ ＜ $\text{[math]}$ ，即 $\text{[math]}$ ， ∴ $\text{[math]}$ 的整数部分是2，小数部分是 $\text{[math]}$ ．
1. （1） $\text{[math]}$ 的整数部分是，小数部分是；
2. （2）如果 $\text{[math]}$ 的小数部分是a， $\text{[math]}$ 整数部分是b，求 $\text{[math]}$ 的值；
3. （3）已知 $\text{[math]}$ ，其中x是整数，且 $\text{[math]}$ ，求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题