河南省信阳市商城县2022年中招数学一模试卷

更新时间：2024-07-13 浏览次数：102 类型：中考模拟

一、单选题

1. (2022·平凉模拟) －2022的倒数是（）

A . －2022 B . 2022 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·商城模拟) 下列问题中，适合抽样调查的是（）

A . “双十一”期间某网店的当日销售额 B . 神舟十三号飞船的零部件检查 C . “7•20”特大暴雨河南省受损的农作物面积 D . 东京奥运会乒乓球比赛用球的合格率

答案解析收藏纠错 + 选题
3. (2022·商城模拟) 下列几何体的三视图中，俯视图与主视图一定一致的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·商城模拟) 如图所示，AB//CD，∠α＝35°，∠C＝∠D，则∠A的度数是（）

A . 35° B . 145° C . 155° D . 55°

答案解析收藏纠错 + 选题
5. (2022·商城模拟) 新型冠状病毒呈球形或椭圆形，有包膜，直径大约是100m.新型冠状病毒是一种先前未在人类中发现的冠状病毒，显微镜下看呈皇冠形，所以称为冠状病毒.既往已知感染人的冠状病毒有六种，新型冠状病毒属于β属的冠状病毒，属于第七种冠状病毒.将100nm（1nm＝10^﹣⁹m）用科学记数法表示为（）

A . 1×10^﹣⁷m B . 1×10^﹣⁸m C . 1×10^﹣⁹m D . 1×10^﹣⁶m

答案解析收藏纠错 + 选题
6. (2022八上·信阳开学考) 《九章算术》是中国古代数学著作之一，书中有这样的一个问题：今有甲、乙二人持钱不知其数.甲得乙半而钱五十，乙得甲太半而钱亦五十.问甲、乙持钱各几何？题意为：今有甲、乙二人，不知其钱包里有多少钱.若乙把其一半的钱给甲，则甲的钱数为50；而甲把其 $\text{[math]}$ 的钱给乙，则乙的钱数也能为50，问甲、乙各有多少钱？解：设甲原有钱数为x，乙原有钱数为y，依题意可得方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·萧山模拟) 将分别标有“中”“国”…“全”“面”“小”“康”汉字的六个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀，随机摸出一球，然后放回，再随机摸出一球，两次摸出的球上的汉字是“小”和“康”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九下·荆州月考) 函数 $\text{[math]}$ 的图象如图所示，则关于x的一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 没有实数根 B . 有两个相等的实数根 C . 有两个不相等的实数根 D . 无法确定

答案解析收藏纠错 + 选题
9. (2022·商城模拟) 如图，在平面直角坐标系中放置一菱形OABC，已知∠ABC＝60°，点B在y轴上，OA＝1，将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2021次，点B的落点依次为B₁ ， B₂ ， B₃ ， ……，则B₂₀₂₁的坐标为（）

A . （1010，0） B . （1345， $\text{[math]}$ ） C . （ $\text{[math]}$ ， $\text{[math]}$ ） D . （1346，0）

答案解析收藏纠错 + 选题
10. (2022·商城模拟) 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2 $\text{[math]}$ ，CD⊥AB于点D ．点P从点A出发，沿A→D→C的路径运动，运动到点C停止，过点P作PE⊥AC于点E ，作PF⊥BC于点F ．设点P运动的路程为x ，四边形CEPF的面积为y ，则能反映y与x之间函数关系的图象（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2022·商城模拟) 请写出一个大于3小于5的无理数：.

答案解析收藏纠错 + 选题
12. (2022·商城模拟) 某函数满足当自变量x＝1时，函数值y＝0.写出一个满足条件的一次函数表达式：.

答案解析收藏纠错 + 选题
13. (2022·商城模拟) 如图所示，在△ABC中，∠B＝90°，AB＝BC＝4，D，E，F分别是AC，BC，AB边上的点，且∠EDF＝45°，DE＝DF，则AF+CE＝.

答案解析收藏纠错 + 选题
14. (2022·商城模拟) 如图，图1是由若干个相同的图形（图2）组成的美丽图案的一部分，图2中，图形的相关数据：半径OA=2cm，∠AOB=120°．则图2的周长为cm（结果保留π）．

答案解析收藏纠错 + 选题
15. (2022·商城模拟) 在矩形ABCD中，AB＝4，BC＝2，点E在线段BC上，连接AE，过点B作BF⊥AE交线段CD于点F.以BE和BF为邻边作平行四边形BEHF，当点E从B运动到C时，点H运动的路径长为.

答案解析收藏纠错 + 选题

三、解答题

16. (2022·商城模拟)
1. （1）计算： $\text{[math]}$ ；
2. （2）化简： $\text{[math]}$ .
答案解析收藏纠错 + 选题
17. (2022·商城模拟) 2021年秋季教育部明确提出，要减轻义务教育阶段学生的作业负担，学生的校外培训负担.依据政策要求，初中书面作业平均完成时间不超过90分钟，学生每天的完成作业时长不能超过2小时.某中学为了积极推进教育部的新政策实施，对本校学生的作业情况进行了抽样调查，统计结果如图所示：
1. （1）这次抽样共调查了 ▲ 名学生，并补全条形统计图；
2. （2）计算扇形统计图中表示作业时长为2.5小时对应的扇形圆心角度数；
3. （3）若该中学共有学生3000人，请据此估计该校学生的作业时间不少于2小时的学生人数；
4. （4）通过本次调查，你认为该学校作业布置是否满足教育部的“双减”政策要求？请说明理由，并给出相应的建议.
答案解析收藏纠错 + 选题
18. (2022·商城模拟) 弦切角定理（弦切角等于它所夹的弧所对的圆周角）在证明角相等、线段相等、线段成比例等问题时，有非常重要的作用，为了说明弦切角定理的正确性，小明同学进行了以下探索过程：
问题的提出：若一直线与圆相交，过交点作圆的切线，则此切线与直线的交角中的任意一个称为直线和圆的交角，其中所夹弧为劣弧的角为劣交角，所夹弧为优弧的角为优交角.直线和圆的交角有以下性质：直线和圆的交角等于所夹弧所对的圆周角.
问题的证明：（只证明劣交角即可）
1. （1）请将不完整的已知和求证补充完整，并写出证明过程；
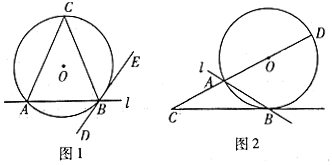
  已知：如图1，直线l与⊙O相交于点A，B，过点B作 ▲ .
  求证：∠ABD＝ ▲ .
2. （2）如图2，直线l与⊙O相交于点A，B，AD为⊙O的直径，BC切⊙O于点B，交DA的延长线于点C，若AD＝BC，AC＝2，求⊙O的半径.
答案解析收藏纠错 + 选题
19. (2022·商城模拟) 如图，点P为函数 $\text{[math]}$ 与函数 $\text{[math]}$ 图象的交点，点P的纵坐标为4， $\text{[math]}$ 轴，垂足为点B.
1. （1）求m的值；
2. （2）点M是函数 $\text{[math]}$ 图象上一动点，过点M作 $\text{[math]}$ 于点D，若 $\text{[math]}$ ，求点M的坐标.
答案解析收藏纠错 + 选题
20. (2022·商城模拟) 某汽车贸易公司销售A，B两种型号的新能源汽车，A型车进货价格为每台12万元，B型车进货价格为每台15万元，该公司销售2台A型车和5台B型车，可获利3.1万元，销售1台A型车和2台B型车，可获利1.3万元.
1. （1）求销售一台A型、一台B型新能源汽车的利润各是多少万元？
2. （2）该公司准备用300万元资金，采购A，B两种新能源汽车，可能有多少种采购方案？
3. （3）该公司准备用不超过300万，采购A，B两种新能源汽车共22台，问最少需要采购A型新能源汽车多少台？
答案解析收藏纠错 + 选题

21. (2022·商城模拟) 小明根据学习函数的经验，对函数y＝|x²﹣2x|﹣2的图象与性质进行了探究，下面是小明的探究过程，请补充完整：

x	…	﹣2	﹣1	0	1	2	3	4	…
y	…	6	m	﹣2	﹣1	﹣2	n	6	…

（1）在给定的平面直角坐标系中；画出这个函数的图象，
①列表，其中m＝ ▲ ， n＝ ▲ .
②描点：请根据表中数据，在如图所示的平面直角坐标系中描点：
③连线：画出该函数的图象.
（2）写出该函数的两条性质：.
（3）进一步探究函数图象，解决下列问题：
①若平行于x轴的一条直线y＝k与函数y＝|x²﹣2x|﹣2的图象有两个交点，则k的取值范围是；

②在网格中画出y＝x﹣2的图象，直接写出方程|x²﹣2x|﹣2＝x﹣2的解为 .

答案解析收藏纠错 + 选题

22. (2022·商城模拟) 如图，直线 $\text{[math]}$ 与x轴交于点A（3，0），与y轴交于点B，抛物线 $\text{[math]}$ 经过点A，B.
1. （1）求点B的坐标和抛物线的表达式；
2. （2） P（x₁ ， y₁），Q（4，y₂）两点均在该抛物线上，若y₁≥y₂ ，求P点的横坐标x₁的取值范围；
3. （3）点M为直线AB上一动点，将点M沿与y轴平行的方向平移一个单位长度得到点N，若线段MN与抛物线只有一个公共点，直接写出点M的横坐标的取值范围.
答案解析收藏纠错 + 选题
23. (2022·商城模拟) 在△ABC中，∠ACB＝90°，AC＝BC，点D是直线AB上的一动点（不与点A，B重合），连接CD，在CD的右侧以CD为斜边作等腰直角三角形CDE，点H是BD的中点，连接EH.
1. （1）如图1，当点D是AB的中点时，线段EH与AD的数量关系是，EH与AD的位置关系是；
2. （2）如图2，当点D在边AB上且不是AB的中点时，（1）中的结论是否仍然成立？若成立，请仅就图2中的情况给出证明；若不成立，请说明理由；
3. （3）若AC＝BC＝2 $\text{[math]}$ ，其他条件不变，连接AE，BE.当△BCE是等边三角形时，请直接写出△ADE的面积.
答案解析收藏纠错 + 选题