北京市西城区2020-2021学年八年级下学期期末数学试题

更新时间：2024-07-13 浏览次数：106 类型：期末考试

一、单选题

1. (2024八下·包河期末) 若 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是（）

A . x＜4 B . x≥4 C . x＞4 D . x≥0

答案解析收藏纠错 + 选题
2. (2021八下·西城期末) 如图，在▱ABCD中，∠C＝70°，DE⊥AB于点E，则∠ADE的度数为（）

A . 30° B . 25° C . 20° D . 15°

答案解析收藏纠错 + 选题
3. (2024八下·包河期末) 下列各式中是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·包河期末) 下列线段a，b，c组成的三角形中，能构成直角三角形的是（）

A . a＝1，b＝2，c＝2 B . a＝2，b＝3，c＝4 C . a＝3，b＝4，c＝6 D . a＝1，b＝1，c＝ $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·新罗期末) 在一次学校田径运动会上，参加男子跳高的20名运动员的成绩如表所示：
成绩/m
1.55
1.60
1.65
1.70
1.75
1.80
人数
1
4
3
4
6
2
这些运动员成绩的众数是（）

A . 1.65 B . 1.70 C . 1.75 D . 1.80

答案解析收藏纠错 + 选题
6. (2021八下·西城期末) 如图，在Rt△ABC中，∠ACB＝90°，AC＝1，BC＝4，D是AB边的中点，则CD的长为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·包河期末) 下列命题中，正确的是（）

A . 有一组对边相等的四边形是平行四边形 B . 有两个角是直角的四边形是矩形 C . 对角线互相垂直的四边形是菱形 D . 对角线互相垂直且相等的平行四边形是正方形

答案解析收藏纠错 + 选题
8. (2024八下·包河期末) 学校组织校科技节报名，每位学生最多能报3个项目．下表是某班30名学生报名项目个数的统计表：
报名项目个数
0
1
2
3
人数
5
14
a
b
其中报名2个项目和3个项目的学生人数还未统计完毕．无论这个班报名2个项目和3个项目的学生各有多少人，下列关于报名项目个数的统计量不会发生改变的是（）

A . 中位数，众数 B . 平均数，方差 C . 平均数，众数 D . 众数，方差

答案解析收藏纠错 + 选题
9. (2021八下·西城期末) 如图，在平面直角坐标系xOy中，菱形OABC的顶点A的坐标为（0，2），顶点B，C在第一象限，且点C的纵坐标为1，则点B的坐标为（）

A . （2，3） B . （ $\text{[math]}$ ， 3） C . （ $\text{[math]}$ ， 2 $\text{[math]}$ ） D . （ $\text{[math]}$ ， 3）

答案解析收藏纠错 + 选题
10. (2021八下·西城期末) 图1，四边形ABCD是平行四边形，连接BD，动点P从点A出发沿折线AB→BD→DA匀速运动，回到点A后停止．设点P运动的路程为x，线段AP的长为y，图2是y与x的函数关系的大致图象，则▱ABCD的面积为（）

A . 24 $\text{[math]}$ B . 16 $\text{[math]}$ C . 12 $\text{[math]}$ D . 36

答案解析收藏纠错 + 选题

二、填空题

11. (2021八下·西城期末) 计算：（ $\text{[math]}$ ）²＝．

答案解析收藏纠错 + 选题
12. (2021八下·西城期末) 已知正方形ABCD的对角线AC的长为3 $\text{[math]}$ ，则正方形ABCD的边长为．

答案解析收藏纠错 + 选题
13. (2023八下·和平期末) 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E是AB的中点， $\text{[math]}$ ，则AD的长为cm．

答案解析收藏纠错 + 选题
14. (2024八下·合肥期中) 已知n是正整数，且 $\text{[math]}$ 也是正整数，写出一个满足条件的n的值：n＝．

答案解析收藏纠错 + 选题
15. (2021八下·西城期末) 如图，在矩形ABCD中，点E在边AD上，EF平分∠AEC交BC于点F．若AD＝7，AE＝CD＝3，则BF的长为．

答案解析收藏纠错 + 选题
16. (2021八下·西城期末) 用4张全等的直角三角形纸片拼接成如图所示的图案，得到两个大小不同的正方形．若正方形ABCD的面积为10，AH＝3，则正方形EFGH的面积为．

答案解析收藏纠错 + 选题
17. (2021八下·西城期末) 为了满足不同顾客对保温时效的要求，保温杯生产厂家研发了甲、乙两款保温杯．现从甲、乙两款中各随机抽取了5个保温杯，测得保温时效（单位：h）如表：
甲组
11
12
13
14
15
乙组
x
6
7
5
8
如果甲、乙两款保温杯保温时效的方差是相等的，那么x＝．

答案解析收藏纠错 + 选题
18. (2021八下·西城期末) 如图，点C在线段AB上，△DAC是等边三角形，四边形CDEF是正方形．
1. （1） ∠DAE＝°；
2. （2）点P是线段AE上的一个动点，连接PB，PC．若AC＝2，BC＝3，则PB＋PC的最小值为．
答案解析收藏纠错 + 选题
19. (2021八下·西城期末) 在学习二次根式的过程中，小腾发现有一些特殊无理数之间具有互为倒数的关系
例如：由（ $\text{[math]}$ ＋1）（ $\text{[math]}$ ﹣1）＝1，可得 $\text{[math]}$ ＋1与 $\text{[math]}$ ﹣1互为倒数，即 $\text{[math]}$ ＝ $\text{[math]}$ ﹣1， $\text{[math]}$ ＝ $\text{[math]}$ ＋1，类似地， $\text{[math]}$ ＝ $\text{[math]}$ ﹣ $\text{[math]}$ ， $\text{[math]}$ ＝ $\text{[math]}$ ＋ $\text{[math]}$ ； $\text{[math]}$ ＝2﹣ $\text{[math]}$ ， $\text{[math]}$ ＝2＋ $\text{[math]}$ ；⋯．
根据小腾发现的规律，解决下列问题：
1. （1） $\text{[math]}$ ＝， $\text{[math]}$ ＝；（n为正整数）
2. （2）若 $\text{[math]}$ ＝2 $\text{[math]}$ ﹣m，则m＝；
3. （3）计算： $\text{[math]}$ ＝．
答案解析收藏纠错 + 选题

三、解答题

20. (2021八下·西城期末) 计算：
1. （1） 3 $\text{[math]}$ × $\text{[math]}$ ；
2. （2） $\text{[math]}$ ＋ $\text{[math]}$ ÷ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2021八下·西城期末) 如图，在▱ABCD中，点E，F分别在边AB，CD上，BE＝DF，EF与对角线AC相交于点O．求证：OE＝OF．

答案解析收藏纠错 + 选题
22. (2021八下·西城期末) 我国古代数学著作《九章算术》中有这样一个问题：今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适与岸齐．问水深、葭长各几何．（1丈＝10尺）
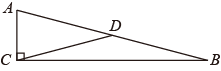
大意是：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．水的深度与这根芦苇的长度分别是多少？

将这个实际问题转化为数学问题，根据题意画出图形（如图所示），其中水面宽AB＝10尺，线段CD，CB表示芦苇，CD⊥AB于点E．
1. （1）图中DE＝尺，EB＝尺；
2. （2）求水的深度与这根芦苇的长度．
答案解析收藏纠错 + 选题
23. (2021八下·西城期末) 在Rt△ABC中，∠ACB＝90°，点D是边AB上的一个动点，连接CD．作AE∥DC，CE∥AB，连接ED．
1. （1）如图1，当CD⊥AB时，求证：AC＝ED；
2. （2）如图2，当D是AB的中点时，
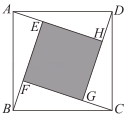
  ①四边形ADCE的形状是；（填“矩形”、“菱形”或“正方形”）
  
  ②若AB＝10，ED＝8，则四边形ADCE的面积为．
答案解析收藏纠错 + 选题
24. (2021八下·西城期末) 对于函数y＝|x﹣1|，小芸探究了该函数的部分性质，下面是小芸的探究过程，请补充完整：
1. （1） ①对于函数y＝|x﹣1|，当x≤1时，y＝﹣x＋1；当x＞1时，y＝　 ▲ 　；
  ②当x≤1时，函数y＝|x﹣1|的图象如图所示，请在图中补全函数y＝|x﹣1|的图象；
2. （2）当y＝3时，x＝；
3. （3）若点A（﹣1，y₁）和B（x₂ ， y₂）都在函数y＝|x﹣1|的图象上，且y₂＞y₁ ，结合函数图象，直接写出x₂的取值范围．
答案解析收藏纠错 + 选题

25. (2021八下·西城期末) 某校七年级和八年级学生人数都是200人，学校想了解这两个年级学生的阅读情况，分别从每个年级随机抽取了40名学生进行调查，收集了这80名学生一周阅读时长的数据，并对数据进行了整理、描述和分析．下面给出了部分信息．

a．七、八年级各抽取的40名学生一周阅读时长统计图（不完整）如下（两个年级的数据都分成6组：0≤x＜2，2≤x＜4，4≤x＜6，6≤x＜8，8≤x＜10，10≤x＜12）：

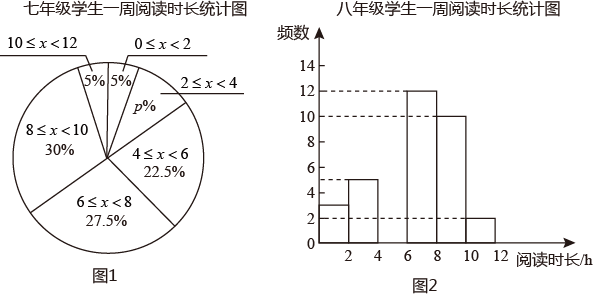
b．八年级学生一周阅读时长在6≤x＜8这一组的数据是：

6；6；6；6；6.5；6.5；7；7；7；7；7.5；7.5

c．七、八年级学生一周阅读时长的平均数、中位数和众数如下：

年级	平均数	中位数	众数
七年级	6.225	7	7
八年级	6.375	m	8

根据以上信息，回答下列问题：

（1）图1中p%＝%；
（2） ①补全八年级学生一周阅读时长统计图（图2）；
②上表中m的值为　▲ 　．
（3）将收集的这80名学生的数据分年级由大到小进行排序，其中有一名学生一周阅读时长是6.5小时，排在本年级的前20名，由此可以推断他是年级的学生；（填“七”或“八”）
（4）估计两个年级共400名学生中，一周阅读时长不低于8小时的人数．

答案解析收藏纠错 + 选题

26. (2021八下·西城期末) 在平面直角坐标系xOy中，点A在x轴的正半轴上，点B在第一象限，作射线OB．给出如下定义：如果点P在∠BOA的内部过点P作PM⊥OA于点M，PN⊥OB于点N，那么称PM与PN的长度之和为点P关于∠BOA的“内距离”，记作d（P，∠BOA），即d（P，∠BOA）＝PM＋PN．
1. （1）如图1，若点P（3，2）在∠BOA的平分线上，则PM＝，PN＝，d（P，∠BOA）＝；
2. （2）如图2，若∠BOA＝75°，点C（a，a）（其中a＞0）满足d（C，∠BOA）＝2＋ $\text{[math]}$ ，求a的值；
3. （3）若∠BOA＝60°，点Q（m，n）在∠BOA的内部，用含m，n的式子表示d（Q，∠BOA），并直接写出结果．
答案解析收藏纠错 + 选题
27. (2021八下·西城期末) 已知∠MON＝90°，点A是射线ON上的一个定点，点B是射线OM上的一个动点，且满足OB＞OA．点C在线段OA的延长线上，且AC＝OB．
1. （1）如图1，CD∥OB，CD＝OA，连接AD，BD；
  ①△AOB与△全等，∠OBA＋∠ADC＝°；
  
  ②若OA＝a，OB＝b，则BD＝；（用含a，b的式子表示）
2. （2）如图2，在线段BO上截取BE，使BE＝OA，连接CE．若∠OBA＋∠OCE＝β，当点B在射线OM上运动时，β的大小是否会发生变化？如果不变，请求出这个定值；如果变化，请说明理由．
答案解析收藏纠错 + 选题
28. (2021八下·西城期末) 如图，△ABC和△DCE都是等边三角形，∠ACD＝α（60°＜α＜120°），点P，Q，M分别是AD，CD，CE的中点．
1. （1）求∠PQM的度数；（用含α的式子表示）
2. （2）若点N是BC的中点，连接NM，NP，PM，求证：△PNM是等边三角形．
答案解析收藏纠错 + 选题
29. (2021八下·西城期末) 在平面直角坐标系xOy中，对于任意两点M（x₁ ， y₁），N（x₂ ， y₂），我们将|x₁﹣x₂|＋2|y₁﹣y₂|称为点M与点N的“纵2倍直角距离”，记作dMN．
例如：点M（﹣2，7）与N（5，6）的“纵2倍直角距离”dMN＝|﹣2﹣5|＋2|7﹣6|＝9，
1. （1） ①已知点P₁（1，1），P₂（﹣4，0），P₃（0， $\text{[math]}$ ），则在这三个点中，与原点O的“纵2倍直角距离”等于3的点是　 ▲ 　；
  ②已知点P（x，y），其中y≥0，若点P与原点O的“纵2倍直角距离”dPO＝3，请在下图中画出所有满足条件的点P组成的图形．
2. （2）若直线y＝2x＋b上恰好有两个点与原点O的“纵2倍直角距离”等于3，求b的取值范围；
3. （3）已知点A（1，1），B（3，1），点T（t，0）是x轴上的一个动点，正方形CDEF的顶点坐标分别为C（t﹣ $\text{[math]}$ ， 0），D（t， $\text{[math]}$ ），E（t＋ $\text{[math]}$ ， 0），F（t，﹣ $\text{[math]}$ ）．若线段AB上存在点G，正方形CDEF上存在点H，使得dGH＝5，直接写出t的取值范围．
答案解析收藏纠错 + 选题