安徽省合肥市新站高新区2022年中考一模数学试题

更新时间：2022-04-30 浏览次数：129 类型：中考模拟

一、单选题

1. (2022·合肥模拟) － $\text{[math]}$ 的绝对值是（）

A . － $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D － $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·合肥模拟) 下列运算中正确的是（）

A . （－a²）³＝－a⁵ B . a³•a⁴＝a¹² C . 3a²－2a²＝1 D . a⁶÷a²＝a⁴

答案解析收藏纠错 + 选题
3. (2022九下·龙凤期中) 一个正方体沿四条棱的中点切割掉一部分后，如图所示，则该几何体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·合肥模拟) 2022年2月8日，中国运动员谷爱凌在自由式滑雪女子大跳台决赛中夺冠，这是北京冬奥会中中国队在雪上项目中夺得的首枚金牌．滑雪大跳台项目场馆，坐落在北京市首钢园区的北京冬季奥林匹克公园，园区总占地面积171.2公顷即1712000平方米，将1712000用料学记数法表示为（）

A . 1712×10³ B . 1.712×10⁷ C . 1.712×10⁶ D . 0.1712×10⁷

答案解析收藏纠错 + 选题
5. (2022·合肥模拟) 如图，AB//CD//EF，若∠CEF＝105°，∠BCE＝55°，则∠ABC的度数为（）

A . 110° B . 115° C . 130° D . 135°

答案解析收藏纠错 + 选题
6. (2023·任城模拟) 如图，正六边形 $\text{[math]}$ 的边长为2，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 的长为半径画弧，得 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·合肥模拟) 已知a、b、c均为实数，且满足a＋b＋c＝15，ab＋ac＝50，则b＋c－a的值为（）

A . 5 B . －5 C . 5或－5 D . 3或 7

答案解析收藏纠错 + 选题
8. (2022·合肥模拟) 某人购进一批苹果到集贸市场零售，已知卖出的苹果数量y（千克）与售价x（元）之间的关系如图所示，若成本5元/千克，现以8元/千克卖出，能挣得钱数为（）

A . 55元 B . 155元 C . 165元 D . 440元

答案解析收藏纠错 + 选题
9. (2022·合肥模拟) 如图，一次函数y＝－x的图象与反比例函数y＝－ $\text{[math]}$ 图象交于A和B两点，则不等式－x＞－ $\text{[math]}$ 的解集是（）

A . x＜－2 B . x＜2 C . －2＜x＜2 D . 0＜x＜2或x＜－2

答案解析收藏纠错 + 选题
10. (2022·合肥模拟) 在等边△ABC中，AB＝2，点D是BC边的中点，点E是AC边上一个动点，连接DE，将DE绕点D顺时针旋转90°，得到DE'，连接CE'，则CE'的最小值是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·广州月考) 计算：( $\text{[math]}$ )²=。

答案解析收藏纠错 + 选题
12. (2023·日照) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2022·合肥模拟) 如图，在Rt△ACB中，AC＝6、AB＝10，AD平分∠CAB，BD⊥AD，AD的值是．

答案解析收藏纠错 + 选题
14. (2022·合肥模拟) 直线y＝－x＋3与x轴交于点A、与y轴交于点B，经过A、B两点的二次函数y＝－x²＋2x＋c的图象与x轴的另一个交点为点C，P是抛物线上第一象限内的点，连接OP，交直线AB于点Q，设点P的横坐标为m，PQ与OQ的比值为n．
1. （1） c＝；
2. （2） n的最大值为．
答案解析收藏纠错 + 选题
15. (2022·合肥模拟) 如图①，我们把一个矩形称作一个基本图形，把矩形的顶点及其对称中心称作基本图形的特征点，显然这样的基本图形共有5个特征点，将此基本图形不断地复制并平移，使得相邻两个基本图形的两个特征点重合，这样得到第2个图；第3个图；……；
1. （1）观察以上图形并完成下表：
  基本图形的个数
  1
  2
  3
  4
  …
  特征点的个数
  5
  8
  11
  …
  猜想：在第n个图中特征点的个数为（用含n的代数式表示）．
2. （2）在平面直角坐标系中，点A、点B是坐标轴上的两点，且OA＝1，以OA、OB为边作一个矩形，其一条对角线所在直线的解析式为y＝ $\text{[math]}$ x，将此矩形作为基本图形不断复制和平移，如图②所示，若各矩形的对称中心分别为O₁、O₂、O₃、……，则O₂₀₂₂的坐标为．
答案解析收藏纠错 + 选题

三、解答题

16. (2022·合肥模拟) 解不等式组 $\text{[math]}$ ，并把解集在数轴上表示出来．

答案解析收藏纠错 + 选题
17. (2022·合肥模拟) 在平面直角坐标系中，ΔABC的三个顶点的坐标分别是A（1，3）、B（4，1）、C（1，1）．
1. （1）画出将△ABC沿着x轴方向向左平移5个单位得到的△A₁B₁C₁；
2. （2）以O为位似中心，画出ΔABC的位似图形△A₂B₂C₂ ，使放大前后位似比为1∶2．
答案解析收藏纠错 + 选题
18. (2022·净月模拟) 为保障新冠病毒疫苗接种需求，某生物科技公司开启“加速”模式，生产效率比原先提高了20%，现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天，问原先每天生产多少万剂疫苗？

答案解析收藏纠错 + 选题
19. (2022·合肥模拟) 如图，在东西方向的海岸上有两个相距6海里的码头B，D．某海岛上的观测塔A距离海岸5海里，在A处测得B位于南偏西 $\text{[math]}$ 方向．一艘渔船从D出发，沿正北方向航行至C处，此时在A处测得C位于南偏东 $\text{[math]}$ 方向，求此时观测塔A与渔船C之间的距离（结果精确到0.1海里）．
（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2022·合肥模拟) 如图1，四边形ABCD内接于⊙O，BD为直径，弧AD上存在点E，满足弧AE＝弧CD，连结BE并延长交CD的延长线于点F，BE与AD交于点G
1. （1）若∠DBC＝ $\text{[math]}$ ，请用含 $\text{[math]}$ 的代数式表示∠AGB；
2. （2）如图2，连接CE，CE＝BG，求证：EF＝DG；
答案解析收藏纠错 + 选题
21. (2022·合肥模拟) 九（1）班针对“你最向往的研学目标”的问题对全班学生进行了调查（共提供A、B、C、D四个研学目标，每名学生从中分别选一个目标），并根据调查结果列出统计表绘制扇形统计图.
男、女生最向往的研学目标人数统计表
目标
A
B
C
D
男生（人数）
7
m
2
5
女生人数
9
4
2
n
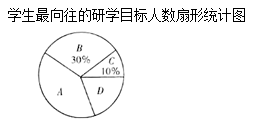
根据以上信息解决下列问题：
1. （1） m=；n=；
2. （2）扇形统计图中A所对应扇形的圆心角度数为；
3. （3）从最向往的研学目标为C的4名学生中随机选取2名学生参加竞标演说，求所选取的2名学生中恰好有一名男生、一名女生的概率.
答案解析收藏纠错 + 选题
22. (2022·合肥模拟) 如图，抛物线y＝mx²＋（m²＋3）x－（6m＋9）与x轴交于点A、B，与y轴交于点C，已知B（3，0）
1. （1）求m的值和直线BC对应的函数表达式；
2. （2）点P是直线BC上方的抛物线上点，若S_ΔPBC＝S_ΔABC，请直接写出点P的坐标；
3. （3） Q为抛物线上一点，若∠ACQ＝45°，求点Q的坐标；
答案解析收藏纠错 + 选题
23. (2022·合肥模拟) 在四边形ABCD中，∠ABC＝90°，AB＝BC，对角线AC、BD相交于点E，过点C作CF垂直于BD，垂足为F，且CF＝DF
1. （1）求证：ΔACD∽△BCF；
2. （2）如图2，连接AF，点P、M、N分别为线段AB、AF、DF的中点，连接PM、MN、PN．
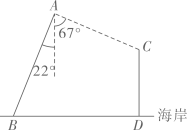
  ①求证：∠PMN＝135°；
  ②若AD＝2 $\text{[math]}$ ，求ΔPMN的面积；
答案解析收藏纠错 + 选题