①试验条件不会影响某事件出现的频率；
②在相同的条件下试验次数越多，就越有可能得到较精确的估计值，但各人所得的值不一定相同；
③如果一枚骰子的质量分布均匀，那么抛掷后每个点数出现的机会均等；
④抛掷两枚质量分布均匀的相同的硬币，出现“两个正面”、“两个反面”、“一正一反”的机会相同．
的正整数（每次只能写一个数），规定禁止在黑板上写已经写过的数的约数，最后不能写的为失败者，如果甲写第一个，那么，甲写数字（ ）时有必胜的策略．建立模型：为解决上面的“问题”，我们先建立并研究下面从口袋中摸球的数学模型：
①我们首先考虑最简单的情况：既要确保从口袋中摸出的小球至少有2个是同色的，则最少需摸出多少个小球？
假若从袋中随机摸出3个小球，它们的颜色可能会出现多种情况，其中最不利的情况就是它们的颜色各不相同，那么只需要再从袋中摸出1个小球就可确保至少有2个小球同色，即最少需要摸出小数的个数是：1+3=4；
②若要确保从口袋中摸出的小球至少有3个是同色的呢？
我们只需要在①的基础上，再从袋中摸出3个小球，就可以确保至少有3个小球同色，即最少需摸出小球的个数是：1+3×2=7
③若要确保从口袋中摸出的小球至少有4个小球同色，即最少需要摸出小球的个数是：1+3×3=10
④若要确保从口袋中摸出的小球至少有a个是同色的呢？即最少需要摸出小球的个数是．
①若要确保摸出的小球至少有2个同色，则最少需摸出小球的个数是；
②若要确保摸出的小球至少有12个同色，则最少需摸出小球的个数是；
③若要确保摸出的小球至少有a个同色（a<50），则最少需摸出小球的个数是；
①若要确保摸出的小球至少有3个同色，则最少需摸出小球的个数是
②若要确保摸出的小球至少有a个同色（a<50），则最少需摸出小球的个数是．
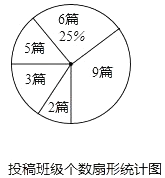
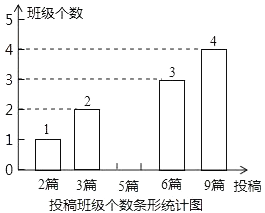
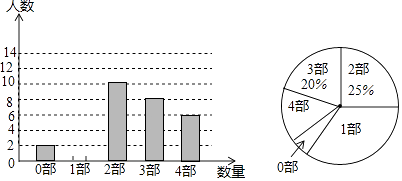
中华文化，源远流长，在文学方面，《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表，被称为“四大古典名著”，某中学为了了解学生对四大古典名著的阅读情况，就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查，根据调查结果绘制城如图所示的两个不完整的统计图，请结合图中信息解决下列问题：
”，小明做了下列三个模拟实验来验证．
